JavaGenes: Evolving Molecular Force Field Parameters

Al Globus, Madhu Menon, and Deepak Srivastava
November 2001

Note: the final draft of this paper was not in a format suitable for the web. This is an early draft in html, but it may contain some errors and needs editing.

Abstract

Accurate molecular dynamics simulation of reactive multi-species systems is important for the design of artificial molecular machines and understanding physical phenomena such as crack propagation, deposition, etching, melting, etc.. For example, the existing reactive hydrocarbon Brenner’s potential has been used to to study vapor deposition, and in the design of gears, hinges, three-way junctions, and bearings. Unfortunately, reactive multi-species potentials are only available for C-H-nobel gas, Si-F, Si-C-Ge and a few other atomic systems. This is not sufficient to design molecular factories of the type envisioned by Drexler [Drexler 1992] or study a wide variety of useful materials. Furthermore, developing reactive multi-species potentials is difficult, time consuming, tedious, failure prone and, thus, rarely attempted.

There are two parts to developing any force field: finding a functional form that reflects the physics and choosing the parameters required by the functional form. Much of the tedium is in the parameterization. We hypothesize that this step can be automated by large genetic algorithm computations on cycle-harvested desktop computers. By automating parameterization, exploration of functional forms should be substantially enhanced.

Given a functional form, the parameters are typically chosen to fit experimental values and/or ab initio calculations. The fitting process can be difficult because, among other reasons, functional forms usually have many local minima that tend to trap search algorithms. We are developing the JavaGenes genetic algorithm to evolve force field parameters. Genetic algorithms are somewhat less likely to fall into local minima than simulated annealing or hill climbing. Furthermore, genetic algorithms can find the pareto front for multiple objectives (e.g., match several experimental results), an impossible task for single solution search strategies. For proof of concept, we have evolved the [Stillinger and Weber 1990] published parameters for Si and F with good results. Using the techniques developed, primarily randomization of the genetic algorithm parameters, we have evolved new Stillinger-Weber parameters for Si fit to semi-empirical quantum code derived energies and forces of silicon clusters. Evolution was driven by energies and forces calculated for 2-6 Si atom clusters, and was able to predict energies for 7-8 atom Si clusters with reasonable accuracy.

Introduction

In this paper we examine using genetic algorithms to parameterize molecular force fields to fit semi-empirical results. The introduction motivates the work, defines the hypothesis, then briefly describes the four underlying software technologies: cycle scavenging, genetic algorithms, semi-empricial quantum calculations (MENON - need text) and molecular force field potential functions. The introduction ends with a description of previous work. We then summarize the method used, present the results, and discuss future work and conclusions. This is followed by is an extremely detailed description of the method, which may be of interest to a few readers.

Motivation

One of nanotechnology's Holy Grails is artificial atomically precise machines and factories with capabilities similar, or superior, to biological systems. The design of atomically precise machines will undoubtedly require superior modeling, including molecular dynamics to examine operations and debug before construction. Furthermore, such machines, if they are ever built, will undoubtedly consist of many atomic species and will make and break bonds. Quantum molecular dynamics for molecular machines with tens of millions of atoms is computationally intractable. However, such large systems can be handled today with classical molecular dynamics if an appropriate potential function is available. Thus, multi-species reactive atomic potential functions are needed. Furthermore, such potential functions are of great immediate utility for the study of deposition, etching, crack propagation, ablation, friction, and other phenomena.

Unfortunately, multi-species reactive potential functions are extremely difficult to develop. The work is hard, tedious, slow, requires great expertise and is failure prone. As a result, only a few such potential functions are available today. These include:

[Tersoff 1989] for carbon-silicon-germanium.
[Stillinger and Weber 1990] for silicon-flourine.
[Brenner 1990] for hydrocarbons.

In the dozen years since these papers were published there has been only incremental progress in expanding the atomic species that are modeled. For example, Brenner's potential can now model carbon and silicon, but only van der Wals forces are available between C and Si atoms. This lack of progress is apparently due the extreme tedium and difficulty of developing these potentials. Furthermore, graduate students usually lack the skills and experience necessary for success, so a large commitment of senior scientist time is needed.

There are two parts to the development of any potential function:

the functional form (for example, F = Gm₁m₂/r² for gravity)
the parameters (for example, G = 6.67390 x 10^-11 m³/kg/s²)

The functional form should reflect the physics of the system of interest, and the parameters should allow the form to fit the available data, although sometimes specific parameters have specific physical meaning. For computational chemistry, relevant data include energies and forces for various atomic conformations calculated by quantum codes, bond lengths, angles, and torsions, minimum structures, lattice constants, vibrational properties, and a host of other experimental data. While development of a physically based functional form for atomic systems is beyond the current capabilities of computer science, fitting parameters to data given a functional form is not. Most of the tedium in multi-species reactive potential function development is in parameter fitting, thinking up functional forms is relatively quick and fun. Thus, if parameter fitting could be automated, then rapid development of broadly applicable potentials may be enabled.

Hypothesis

We hypothesize that multi-species reactive atomic force field potential parameter fitting can be automated using genetic algorithms employing vast quantities of nearly-free CPU cycles. This should allow force field developers to concentrate on the functional form and gathering experimental and computational data to drive evolution and validate the results.

Cycle Scavenging

Most computers in this world spend most of their time doing nothing more useful than updating the clock. Even when a user is directly interacting with a modern PC the CPU is often idle 90% or more of the time. Thus, vast quantities of nearly-free cycles can be scavenged from computers purchased for web browsing, email, document preparation, software development, etc. Batch jobs can be run on these machines at night, weekends, during meeting, and other times when the CPU is otherwise idle. These cycles are nearly-free because the hardware is purchased and maintained by others, only the acquisition and maintenance of the cycle-scavenging system (software and one or a few inexpensive central-manager machines) is necessary.

For the current work, we used the Condor [Litzkow, et al. 1988] cycle scavenger running on about 350 SGI and Sun machines at the NASA Advanced Supercomputing (NAS) Division [www.nas.nasa.gov]. Each workstation runs a daemon that watches user IO and CPU load. When a workstation has been idle for 2 hours, a job from the batch queue is assigned to the workstation and will run until the daemon detects a keystroke, mouse motion, or high non-Condor CPU usage. At that point, the job is removed from the workstation and placed back on the batch queue. The job will eventually run again, although probably on a different machine. Typically, between 100-250 NAS machines are available for batch processing through the NAS Condor pool [www.nas.nasa.gov/Groups/Condor/] at any particular time.

Figure XXX

NAS Condor workstation usage for June 2001. The green represents Condor enabled batch computation. Only the relatively small amount of blue indicates wasted CPU cycles. Note the regular patterns of five red peaks when workstations are in use during normal business hours. The tall blue spikes are upgrade times when Condor calculations were temporarily suspended.

.
Although the NAS Condor pool supplies substantial processing power, it is by no means the largest cycle-scavenging compute facility. The best-known cycle scavenging computation is seti@home [setiathome.ssl.berkeley.edu], currently the largest computation on Earth. This computation runs in background on PCs volunteered by their owners. In September 2001 seti@home was using more than 3 million computers to provide about 23 teraflops/sec.

While cycle-scavenging systems can supply huge amounts of CPU, they are restricted to embarrassingly parallel problems with minimal IO requirements. This is because communication between processors is fairly slow; e.g., ethernet for the NAS Condor pool and 56Kbaud modems for seti@home! However, many important problems fit within these restrictions, including parameter studies, Monte Carlo simulations, and genetic algorithms. For example, much of the data for this paper was generated by running 2500 ~30 minute genetic algorithm (GA) jobs with randomized GA-parameters. This procedure can use thousands of processors with no interprocess communication and minimal disk IO.. As a results, 1000+ CPU hours of computation is routinely accomplished overnight without purchasing any hardware. Furthermore, the NAS Condor system is constantly improving as different groups buy new workstations and retire old ones.

Genetic Algorithms (GA)

Genetic algorithms seek to mimic natural evolution's ability to produce highly functional objects. Natural evolution produces organisms. GAs produce sets of parameters, programs, molecular designs, and many other structures. Our GA, JavaGenes, employs the following algorithm (words in quotes are typical GA terminology):

Represent potential parameters with a set of floating point numbers; each set is called an "individual"
Generate a "population" of individuals with random parameters
Calculate the "fitness" of each individual
Repeat

Randomly, with a bias towards better fitness, select "parents"
Produce "children" from the parents with one of:

"crossover" - combine parts of two parents into a child
"mutation" - modify a single parent

Calculate child fitness
Randomly, with a bias towards less fitness, replace individuals in the population with the children

Until satisfied or exhausted

The vast majority of the CPU time is usually spent in the fitness function.

GAs are search algorithms. In this case, the search is through the space of all reasonable parameters. GAs do not require gradient information, can find a variety of solutions in parallel, and do not require information about the search space. Because GAs generate a large number of solutions (the population), GAs can find the pareto front for multiple optimization objectives. The pareto front is the set of solutions, each of which satisfies at least one objective better than any other solution. This will be important when we hope to evolve parameters to fit not only calculated energies and forces, but also experimental data such as compressibility, surface reconstruction energy, surface bond lengths, vibrational properties, etc.

GAs are easy to implement but hard to use. Also, GAs are not guaranteed to find a satisfactory answer. In addition, there are a wide variety of GA techniques and many techniques have a variety of parameters that can affect the search. Examples of GA parameters include population size and the mix of mutation vs crossover. Thus, choosing the proper GA technique and parameters is a non-trivial problem. We solved this by randomizing the GA parameters.

Furthermore, GAs have a tendency to optimize the fitness function with tricks rather than finding an answer of interest. For example, a robot controller intended to traverse a cluttered environment was evolved with a fitness favoring motion without collision. The most fit individuals found some empty space and went around in small circles indefinitely. GAs can do other strange things. In our study JavaGenes effectively algebraically rearranged the potential function.

Atomic Potentials

Atomic potentials take nuclei position as input and produce energies and forces (the gradient of the energy) as output. Given the force, Newton's Laws of Motion can then be used to calculate molecular dynamics. Energy minima correspond to stable conformations. The energy is generally calculated by some variant of:

Energy = SUM all-two-body-energies + SUM all-three-body-energies + ...

The potentials we are currently interested in ignore terms with more than three bodies. Most potentials do not allow bonds to break so the two and three bodies of interest are fixed for the entire computation. We are interested in reactive potentials where the bonds cannot be predetermined. To reduce computation, reactive potentials often have a cutoff function that forces each term to zero at large atomic separations. This converts the problem from O(n3) to O(n) since only near neighbors need be considered. The Stillinger-Weber (SW) potential used in this paper only considers two and three body terms and has an exponential cutoff. The terms are:

two-body(r) = A(Br^-p - r^-q)cutoff
cutoff = e^C/(r-a); r < a, 0 otherwise

where r is the interatomic distance and all other values are adjustable parameters.

three-body(r_ij,r_jk,theta) = (alpha + lambda(cos(theta) - cos(theta₀))²)cutoff
cutoff = e^gamma/(rij^{- a}1^{)
+ gamma/(r}jk^{- a}1⁾

where rij and rjkare the two interatomic distances, theta is the angle and all other values are adjustable parameters.

In addition, SW has an additional three-body term for fluorine triples. This term is added to the usual three-body term:

delta(r^ijr^jk)^-m cutoff
cutoff = e^beta/(rij^{- a}2^{)
+ beta/(r}jk^{- a}2⁾

Note that this formulation is an algebraic generalization of the form found in [Stillinger and Weber 1990]. This generalization is necessary so that every 2 and 3 body has the same equation (except the extra fluorine three body term). In [Stillinger and Weber 1990] terms = 0 and factors = 1 are left out, but for JavaGenes to evolve new parameters the form must be completely general.

For this paper, the cutoff distance a, a₁, and a₂ are not evolved because they are for optimization. Furthermore, the preferred bond angle theta₀ is not evolved since it is readily available from experiment and theoretical considerations (theta₀ is the tetrahedral angle).

Previous Work

Although it appears that no one has previously used GAs to find parameters for multi-species reactive potentials, two groups have investigated GAs for evolving the MM2 [Mohamadi, et. al. 1990] potential parameters for metal-organic complexes. MM2 is usually used for organic molecules containing no metals. Huttner's group [http://www.uni-heidelberg.de/institute/fak12/AC/huttner/html/startseite.html] at the Anorganisch-Chemisches Institut, Ruprecht-Karls-Universitaet, Heidelberg, Germany has developed force fields for tripod metal compounds using GAs [Hunger, et. al. 1998][Hunger, et. al. 1996] [Hunger and Huttner 1999] to find parameters for the metal component. These studies used compounds containing Mo. The fitness function was based on crystal structure conformations. The GA found minimum structures for each individual set of parameters and compared atomic locations with the crystal structure. Results were successfully validated on new crystal structures and the predicted tortional positions occupied by phenyl groups in the compounds.

[Cundari and Fu 2000] used a similar technique to develop force field parameters for technetium (Tc) complexes. Instead of using differences in predicted atomic locations, Cundari and Fu used the difference of energies predicted by quantum effective core potential calculations and MM2 calculated energies with evolving parameters. Cundari and Fu found that GA evolved parameters could improve the predictive power of MM2 over parameters derived from quantum chemistry calculations by other techniques. Also, MM2 with evolved parameters accuracy on the metal-ligand complexes was comparable to MM2's accuracy on purely organic molecules.

Method Summary

We modified the JavaGenes [Globus, et. al. 1999] genetic algorithm code to evolve force field parameters for the StillingerWeber (SW) functional form. JavaGenes has the following properties:

Individual representation: arrays of double precision floating point numbers representing the Stillinger-Weber parameters. Each parameter is constrained to vary within predetermined limits.
Fitness function: the difference between externally supplied energies and forces and those calculated using the evolving parameters and the SW functional form.
GA technique: steady state GA with tournament selection. Two forms of crossover plus mutation.

To understand this paper, it is important to understand the difference between force-field-parameters (usually called parameters in this paper) and GA-parameters. The force-field-parameters are those found in the Stillinger-Weber functional form. GA-parameters are parameters used to control the search.

At first we ran 30-100 single-workstation GA jobs with identical GA-parameters (except the random number seed) for each force-field-parameter search. These runs used large populations (1000-3000). The GA-parameters that worked for one search (say, Si dimers in the fitness function) would fail in a similar search (for example, Si-F dimers in the fitness function). We then ran thousands of jobs with randomized GA-parameters and small populations (100). This technique worked well for all the searches conducted.

We first reproduced the Stillinger-Weber results using Stillinger-Weber small cluster energies derived from the published Si and F parameters in the fitness function. This showed that the method can find the global, not just the local, minimum. Then, using the same Si clusters, we derived new parameters using a semi-empirical code [Menon and Subbaswamy 1993] to calculate cluster energies and forces. Menon's semi-empirical energies can be used to generate energies and forces for the multi-species potentials of interest (Si-B-N-C-Ge). The Menon semi-empirical code cannot model F so this paper concentrates on Si, although some F results are discussed.

For method details, see the Method Details section below.

Results and Discussion

Reproducing the Published Stillinger-Weber Parameters

Fluorine Parameters

To determine if JavaGenes could evolve correct parameters, we first evolved the Stillinger-Weber parameters using a fitness function based on the published [Stillinger and Weber 90] parameters. The fitness function was the root-mean-square (RMS) of the distance between energies calculated with the published parameters and energies calculated with the evolving parameters. We first fit F dimer energies with 100 pairs of atoms evenly spaced from 0.5 angstroms to the cutoff distance.

Using 51 runs with carefully chosen GA-parameters, it was possible to reproduce the F two-body parameters quite precisely. With F two-body parameters fixed to the best F two-body parameters evolved, the three-body parameters were evolved to fit 51 F2+F2 conformations randomized around the minimum energy conformation. The resulting F parameters were:

F parameters

Parameter	Published value	Evolved Value
A	0.5228	0.5230
B	0.1128	0.1130
C	0.579495	0.579476
p	8.0	7.997
q	4.0	4.001
Three body parameters
alpha	38.295	39.7
lambda	-19.1475	-20.39
gamma	1.738	1.748
delta	0.0818	0.0835
m	4.0	3.978
beta	0.579	0.587

These results required hand-searching through the possible GA-parameters. However, these same GA-parameters performed poorly searching for Si-F two-body parameters. To avoid an extensive hand search through GA-parameters for each subproblem, we adopted an alternate approach: run thousands of jobs with randomized GA-parameters. Although there are many more jobs, we used smaller populations and the runs were considerably faster.

Si, Si-F, and F Two-body Parameters

To evolve two-body parameters, we ran jobs with a population size of 100, 2000 children per generation, and 200 generations with all other GA parameters randomized in each of 2500 batch jobs. Randomized GA-parameters included mutation rate, mutation strength, crossover method, allowed parameter intervals, tournament size, and many others. All 2500 jobs ran in about 12 hours on the NAS Condor pool. Jobs fitting for Si, Si-F, and F dimers were run with these parameters.

The fitness function was not randomized since, otherwise, it would be difficult to compare the results of each job. The fitness function was the difference from precalculated energies at various dimer separations. Near the minimum energy separation, this is calculated as the RMS of the distance between energies. Since energies at short distance have an absolute value orders of magnitude greater than at greater distance, energy comparison on the 'wall' at small separations were compared by:

|a - b| / (|a| + |b|)

where a and b are the energies being compared. This function always returns a value between 0 and 1. This avoids the wall having undue influence on evolution. This measure has pathological properties when a and b are of opposite sign, but on the wall all reasonable parameters generate positive energies.

Table XXX shows results evolving the Si parameters: For two-body parameters we fit the energies of 100 Si dimers spaced 0.5-3.7 angstroms apart.

Table XXX: Si two-body parameters

Parameter	Published value	Evolved value
A	7.0495	-4.21
B	0.602	1.67
C	1.0	1.01
p	4.0	-0.05
q	0.0	4.01

At first the evolved parameters seem to be wildly incorrect, but notice that C is nearly correct and that p and q are (approximately) reversed. Since C is the cutoff parameter, we can ignore the cutoff term and see if the evolved and published parameters are equivalent:

energy(r) = A(Br-p – r^-q)	published	evolved
initial form	7(0.6r^-4 – r^-0)	–4.2(1.67r^-0.05 – r-^4.01)
with A distributed	4.2r^-4 – 7r^-0	–7.014r^-0.05 + 4.2r^-4.01

We see that JavaGenes has effectively performed algebra on the functional form!

Using the same procedure, the F two-body and Si-F two-body parameters were evolved. The published and evolved parameters were:

Table XXX: F two-body and Si-F two-body parameters

Parameter	F published	F evolved	Si-F published	Si-F evolved
A	0.52	0.999	21.2	-5.1
B	0.11	0.167	0.5	2.8
C	0.58	1.27	1.3	1.3
p	8	7.299	3	1.6
q	4	4.01	2	3.4

Here the differences cannot be explained by algebraic rearrangement alone, although p and q are nearly reversed in each case. However, figure XXX shows that the energy and force curves for all three dimers are essentially identical in all three cases:

Figure XXX: comparison of published vs evolved two-body energies and forces

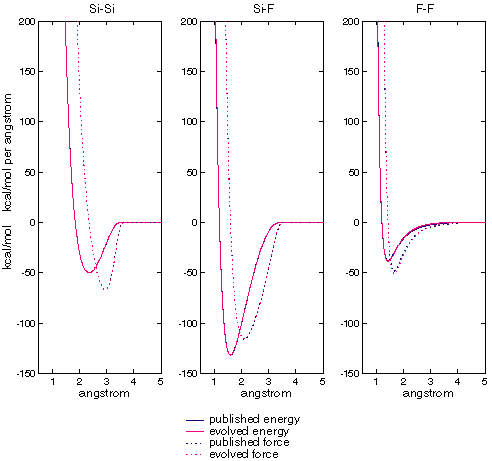
These charts compare the energies and forces generated by published and evolved parameters for Si, F, and Si-F dimers. The horizontal axis is separation, the vertical axis energy and force. Note that in all cases the curves are essentially on top of each other.

A, B, and C are compensating for inaccuracies in p and q. There is, apparently, more than one way to skin an atomic cat.

Silicon Parameters

We then evolved all of the Si parameters using 1000 jobs under the control of a fitness function with 2-6 atom clusters. The 2 atom clusters were the same ones used in the two-body searches. The 3-6 atom clusters were the minimum energy conformation calculated by Menon's semi-empirical code plus many clusters with positions randomized around the minimum energy conformation. Other than the number of jobs and the fitness function, the same GA-parameters were used for this search as for the two-body only search, except that some jobs used an initial population with the two-body parameters set to the best results of the two-body search. The two-body parameters were, however, allowed to evolve (unlike the fluorine study). Table XXX shows the most fit parameters: Table XXX: Si parameters

Parameter	Published value	Evolved Value
A	7.0495	-4.51
B	0.602	1.68
C	1	1.06
p	4	0.015
q	0	4.066
Three body parameters
alpha	0	-1.68
lambda	21	30.5
gamma	1.2	1.289

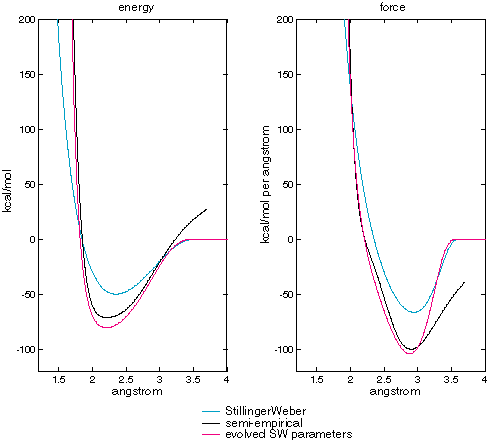
Figure XXX compares the energies generated by Stillinger-Weber with published parameters and those generated by the best evolved individual. This is done for the 2-6 atom clusters used in the fitness function and 7-8 atom clusters that were not. Note that the fit is quite good in both cases.

Figure XXX

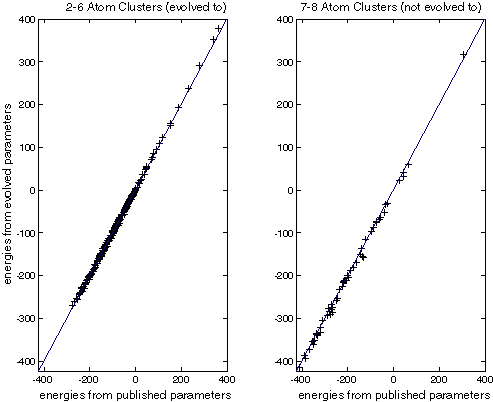
These charts compare the energies calculated for Si clusters. The horizontal axis is the energy calculated with the published SW parameters. The vertical axis is the energy calculated with evolved SW parameters. Crosses on the line indicate a perfect match. All energies are in kcal/mol.

Figure XXX compares the energy and force curves generated by the published and evolved Stillinger-Weber parameters. The match is very close but not quite exact. Genetic algorithms are often good a getting close to an optimum, but not for the final refinement. For computational chemistry, where the data for the fitness function is necessarily a precise reflection of reality this limitation is not serious and perhaps even an advantage.

Figure XXX

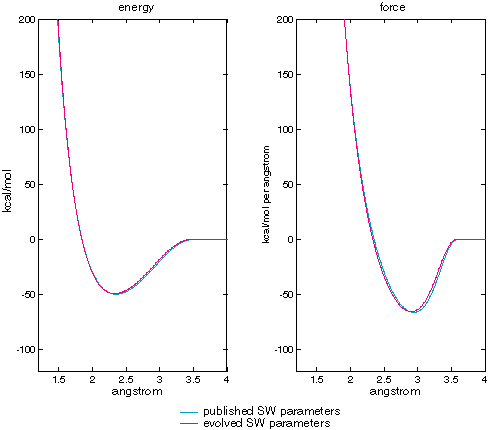
Stillinger-Weber published vs evolved parameters calculating two-body term energy and force as a function of atomic separation.

Figure XXX compares energies for the three-body term only. We see that the fit is quite good, although not as close as for the two-body term. As the three-body term tends to generate smaller energies than the two-body term, it doesn't affect evolution as strongly.

Figure XXX

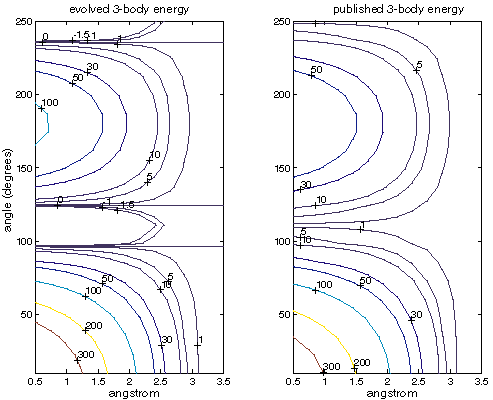
Comparison of the three-body energies for evolved and published SW parameters. The horizontal axis is the distance between the central atom and both other atoms (they are the same distance). The vertical axis is the angle formed around the central atom. Note that the evolved energies go slightly negative as alpha is less than zero. All energies are in kcal/mol.

Evolving Parameters to Match Semi-Empirical Energies

Having validated JavaGenes by reproducing the two- and three-body parameters published by Stillinger-Weber, we turn our attention to the more interesting problem of improving the SW parameters by fitting them to energies and forces calculated by a semi-empirical quantum method [Menon and Subbaswamy 1993]. Menon's semi-empirical code cannot model F, so only Si is examined.

Parameters for the Si dimer were evolved using semi-empirical energies and forces in the fitness function. Since the semi-empirical energies are positive at longer separations, the fitness function fits to forces in this region instead of energies (the SW functional form cannot simultaneously produce a negative minimum energy and positive values in this region). 2500 jobs were run with randomized GA-parameters and the best taken. Table XXX contains the results:

Figure XXX: comparison of parameters published, evolved to SW,
and evolved to semi-empirical dimer energies

Parameter	Published	Evolved to SW	Evolved to semi-empirical
A	7.0495	-4.21	-0.66
B	0.602	1.67	14.23
C	1	1.01	1.48
p	4	-0.05	-2.50
q	0	4.01	18.67

The parameters evolved to the semi-empirical energies and forces are quite different from those evolved to SW. Figure XXX compares the energy and force curves.

Figure XXX

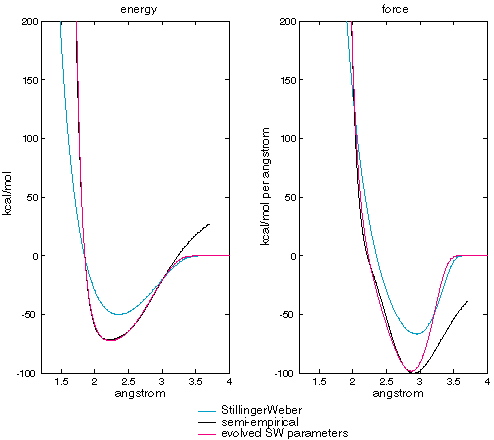
Stillinger-Weber published vs evolved parameters calculating two-body term energy and force as a function of atomic separation.

The evolved parameters match the semi-empirical data much better than the published parameters. The major divergence between SW with evolved parameters and the semi-empirical results is at long separations (> 3 angstrom) where the semi-empirical energies are positive and the Stillinger-Weber form requires energies and forces to go to zero. This requires a change in the fitness function, which is based on differences in energies for most separations, but uses at differences in forces at long separations. There is also a reversal of the derivative of the semi-empirical force curve between 2 and 2.7 angstroms that the SW functional form cannot match.

Having found a good match for the three-body parameters, we evolved all Si parameters to a fitness function based on 2-6 atom clusters. The dimers were handled as above, and the 3-6 atom clusters were the minimum conformation calculated by Menon's semi-empirical code plus a number of conformations randomized around this minimum. This experiment ran 1000 jobs with randomized GA-parameters. One of these parameters was to import the previously evolved two-body parameters as a starting point for part or all of the population.

Figure XXX: comparison of parameters published, evolved to SW,
and evolved to semi-empirical cluster energies

Parameter	Published	Evolved to SW	Evolved to semi-empirical
alpha	0	-1.68	11.7
gamma	21	30.5	10.9
lambda	1.2	1.289	1.38

The best of these jobs not only matched the energies of the 2-6 atom dimers, but also matches a number of 7 and 8 atom clusters randomized around their minimums as seen in figure XXX.

Figure XXX: evolved parameters generate energies very close to semi-empirical energies, even
for clusters not used in the fitness function (not evolved to).

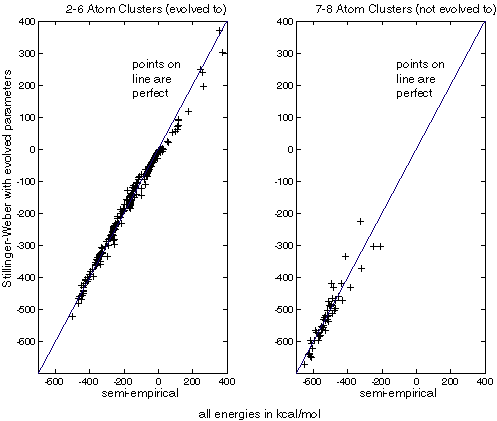
These charts compare the energies calculated for Si clusters. The horizontal axis is the energy calculated with Menon's semi-empirical method. The vertical axis is the energy calculated with evolved SW parameters. Crosses on the line indicate a perfect match.

We see that the energies for 2-6 atom dimers match extremely well, as might be expected since these dimers were used in the fitness function. However, SW with evolved parameters predicted the energies of 7 and 8 atom dimers very well, suggesting that the evolved parameters are at least somewhat transferable. Note that a different set of clusters were used for this study than evolution driven by Stillinger-Weber energies. This is because the randomization code produces a different set of conformations each time it is run.

In addition the predicted energies, figure XXX examines the two-body energies of the new potential.

Figure XXX

Dimer energies and forces for published and evolved SW potential, and Menon's semi-empirical code.

Although they are much closer than energies and forces generated by the published Stillinger-Weber parameters, figure XXX shows that the energies and forces generated by evolved parameters are somewhat different from the semi-empirical energies and forces. Specifically, the minimum energy is lower. By examining the energies on the three-body SW term in isolation we can gain some insight:

Figure XXX

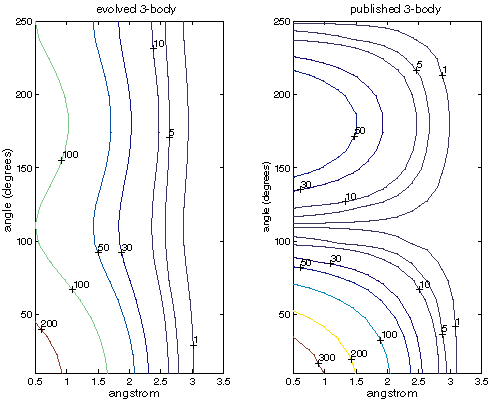
Contour map of Si three-body energies in kcal/mol as a function of angle and separation from the central atom.

Examining the three-body SW term alone, figure XXX shows that the much higher three-body energies may be compensating for the lower two-body energies. Note that these are the energies from the SW three-body term alone and no comparable energy exists in Menon's semi-empirical code. This makes some sense as the cutoff for the SW three-body term depends on the lengths of the two involved bonds. Thus, evolution has moved some of the functionality of the two-body term into the three-body term and sacrificed dimer accuracy as a result. Also note that at long separations the evolved parameters show little preference for any angle.

Future Work

The next step is to evaluate the silicon potential we've developed by calculating equivalent properties and comparing with experimental values. Properly designed, the predictive software can be used in new fitness functions that allow JavaGenes to evolve parameters based on experimental values. We also plan to extend the range of species covered to B, Ge, N, and (with modifications to the functional form) C. These extensions will require JavaGenes to be modified to evolve towards multiple objectives (e.g., match semi-empirical energies and fit vibrational properties, lattice constant, vaporization energy, and surface reconstruction energy).

Conclusion

Genetic algorithms show promise for partially automating parameter generation. A key discovery is that randomization of the GA-parameters is effective. Not all GA-parameters work and searching for the right ones is very time consuming. However, taking advantage of otherwise wasted CPU time by cycle scavengers such as Condor allows the seemingly wasteful use of thousands of GA runs to find the potential parameters of interest. We have demonstrated that JavaGenes can reproduce the Stillinger-Weber published parameters -- or at least the energy and force curves -- to very high precision. We have also demonstrated that we can match energies and forces generated by semi-empirical methods to high accuracy and predict the energies of 7-8 atom clusters not used in the fitness function. Perhaps the time when we have high quality force fields for a large variety of reactive atomic species is not so far off.

Method Details

Since reproducibility is a necessary (but not sufficient) condition for good science, this section is intended to provide sufficient detail to reproduce the results of this paper. This section is placed at the end of the paper since many readers will not be interested in these details.

Run Time Environment

Each run involved many independent genetic algorithm jobs. For the fluorine studies, each job had the same GA-parameters and a different random number seed. For all other studies, most GA-parameters were randomized for each job. Since in a cycle-scavenging environment any given CPU may become unavailable at any moment, each job checkpointed it's state every hour or two. When jobs restarted from a checkpoint, they would be assigned new random GA-parameters. This was done for practical reasons having to do with the current JavaGenes implementation. As a side effect, this means that the runs described here are reproducible only in a statistical sense -- although repeated tries of the same runs gave similar results. Even without randomization of GA parameters, the runs are not perfectly repeatable because of permitted variations in IEEE floating point arithmetic combined with cycle-scavenging. Cycle-scavenging necessarily uses different processors for each run. In our case jobs ran on both SUN and SGI processors and several variants of each (Java really is portable). While perfect repeatability is the norm in computer science, in biology (which GAs attempt to emulate) only statistical repeatability is possible.

At the end of each run, the best individual evolved by any of the jobs was examined. All the results reported above represent the best individual from all jobs for a given run.

JavaGenes Genetic Algorithm

JavaGenes is a steady state tournament selection genetic algorithm. The tournament size is usually two. Individuals to replace are chosen by an anti-tournament of size two.

Steady state means that there is only one population, parents are chosen from this population and children replace individuals in the population.
Tournament selection, with size two, means that each parent is chosen by randomly taking two individuals from the population and choosing the fittest to be the parent. This procedure is repeated for each parent. During GA-parameter randomization the tournament size is probabilistically two or one, one meaning simply that a random individual is chosen as the parent. Size one 'tournaments' helps avoid premature convergence.
An anti-tournament is the same as a tournament except that the least fit individual is chosen for replacement by newly created children.

Representation

JavaGenes represents the potential parameters as a ragged two-dimensional array of double precision floating point numbers. A ragged two-dimensional array has arrays of differing length in the second dimension. The first dimension represents the two- or three-body term of the parameters. For example, one second dimension array might hold the two-body parameters for Si, this would be of length five (A,B,C,p,q); another second dimension array might hold the Si two-body parameters, this would be of length three (alpha, lambda, gamma).

Each parameter is assigned a set of limits within which it is allowed to evolve. In general, A, B, alpha, lambda, and delta shared limits because they are all factors or isolated terms; p, q and m shared limits because they are all exponents, and C, gamma, and beta shared limits because they determine cutoff functions.

Cutoff parameters a₁, a₂, and the preferred angle theta₀ were not evolved. The cutoffs are an optimization for which it is very difficult to write a fast fitness function, and the preferred angle is known from experiment.

Transmission Operators

JavaGenes uses three transmission operators for this study. Transmission operators generate children from parents. These operators are:

Mutation. Mutation requires one parent. A copy of the parent is made and some of the potential parameters are modified. JavaGenes mutation operators take two GA-parameters: the probability a given potential parameters will be changed and the standard deviation of the Gaussian distribution the change will be chosen from. The standard deviation is expressed as a fraction of the interval the potential parameter is allowed to vary within. The mean of the Gaussian is the parental value.
Interval crossover. Interval crossover requires two parents. For each parameter an interval ending at the parental values for that parameter is formed. This interval is increased or decreased by a factor (another GA-parameter). A random number is chosen within this interval. A second GA-parameter can force the child's value to the nearest value with the allowed interval; or allow the child to have an out-of-range potential parameter.

JavaGenes can randomize the transmission operators to use. This is accomplished by representing each transmission operator as an object. These objects can have GA-parameters (for example, probability of mutation for each potential parameter). A random number (within limits) of each kind of transmission operator is put into a list. The transmission operator to use for each child is then randomly chosen from this list.

Fitness Functions

Good GA fitness functions can provide a fitness for any possible individual, no matter how bad, and distinguish between any two individuals, no matter how close. JavaGenes uses three fitness functions forms. All fitness function forms compare energies or forces calculated for some set of atomic conformations with externally supplied energies or forces. The forms are:

Root-mean-square (RMS) deviation from externally supplied energies. This is a well accepted measure of deviation, but has problems when the absolute value of the supplied energy varies wildly, as it does for dimers with very small to very large separations. At very small separations the energies can be in the thousands of kcal/mol, while at large separations the values are near zero. As a result the small separations have an excessive influence. This means the two-body 'wall' might be accurately modeled at the expense of the region near the minimum energy!
Root-mean-square of |a-b|/(|a|+|b|) where a and b are the calculated and externally supplied energies. This expression always returns a value between 0 and 1, eliminating the scaling problem of the previous fitness function. However, if a and b are of opposite signs the value exhibits poor behavior for a fitness function.
Root-mean-square of |a-b|/(|a|+|b|) where a and b are the calculated and externally supplied forces.

Each of these fitness function forms require a set of atomic conformations, small clusters for this study, with 'correct' energies or forces for each conformation.

JavaGenes can form a new fitness function from a weighted linear combination of fitness functions.

While it is possible to randomize the fitness function, and we tried it, this doesn't work very well since it is difficult to compare the results of each run.

GA Parameters

This section details the GA-parameters used in each of the runs discussed above. GA-parameter values placed between brackets, "[" and "]", indicate that the value was chosen randomly within limits. For example, [0.1-0.9] indicates that a GA-parameter was randomly chosen for each job between 0.1 and 0.9 inclusive. Table xxx describes each GA-parameter:

Table xxx

Conformations	Describes the atomic conformations used in the fitness function
Conformation sets	In many studies, several sets of conformations were used. The fitness value for each set was calculated and a linear combination of the fitness for each set was the final fitness
Target energies (and forces) generated by	Describes the source of the energies and forces used in the fitness function. This was always either the Stillinger-Weber potential with published parameters or the Menon semi-empirical code
Energy (and force) comparison	Describes the function used to compare energies and/or forces with the target energies and/or forces
Number of jobs	Number of separate, single-workstation jobs in the run
Population size	Size of the population
Children per generation	Number of children generated for each generation
Number of generations	Number of generations
Transmission operators	Mix of crossover and mutation transmission operators
Interval crossover parameter	For the interval crossover transmission operator, the amount the interval between parental values of a parameter grew or shrank before choosing a random value within the interval.
Mutation frequency	The probability that any one GA-parameter was mutated by the mutation transmission operator.
Mutation standard deviation	The mutation operator modified GA-parameters by choosing randomly from a Gaussian distribution centered on the parental value. This vale is expressed as a fraction of the allowed interval for a GA-parameter.
Stillinger-Weber parameter varies from	the range within which a Stillinger-Weber parameter could vary. Note that the interval crossover operator could be set to ignore this interval.
Immigrants	When searching for both the two- and three-body parameters, JavaGenes can initialize the population with two-body values taken from a run that focused on the two-body parameters. Any fraction (including all) of the initial population could have the two-body terms set this way. Although the initial two-body parameters were set, these parameters were allowed to evolve. Fixing these permanently didn't work well when evolving towards semi-empirical energies and forces.

We now examine list the GA-parameters used for each run discussed in this paper.

Fluorine Studies with Fixed GA-Parameters

There were two runs involved in the fluorine studies, one to find the two-body term using dimers in the fitness function and a second to find the three-body term given the results of the first run. In this case the immigrant capability was not used; rather the two-body parameters were set and not allowed to evolve.

two-body terms

Table XXX contains the GA-parameters used to find the fluorine two-body terms: Table XXX

Conformations	100 dimers evenly spaced from 0.5-4.37 angstroms
Target energies generated by	SW with published parameters
Energy comparison	RMS of \|a - b\| / (\|a\| + \|b\|)
Number of jobs	51
Population size	1000
Children per generation	1000
Number of generations	5000
Transmission operators	75% interval crossover, 25% mutation
Interval crossover parameter	2
Mutation frequency	0.5
Mutation standard deviation	0.25
A,B varies from	-100 to 600
p,q varies from	0 to 24
C varies from	0 to 6

Three-body parameters

These GA-parameters were used to search the fluorine three-body parameters:

Table XXX

Conformations	51 F2+F2 complexes randomized around the low energy conformation
Energy comparison	RMS
Population size	2000
Children per generation	2000
Number of generations	15000

All other parameters were the same as in the fluorine two-body run.

Stillinger-Weber Fitness Studies with Randomized GA-Parameters

Two-body Silicon/Silicon-Fluourine/Fluorine

Table XXX

Conformation sets	30 "wall" dimers evenly spaced from 0.5-1.7 for Si 0.5-1.08 for Si-F 0.5-1.12 for F 70 "rest" dimers evenly space from 1.7-3.8 angstrom for Si 1.08-1.7 angstrom for Si-F 1.12-4.37 angstroms for F
Target energies generated by	SW with published parameters
Energy comparison	RMS of \|a - b\| / (\|a\| + \|b\|) on wall RMS elsewhere Each set of conformations generated a separate value and these were summed to get the fitness
Number of jobs	2501
Population size	100
Children per generation	2000
Number of generations	200
Transmission operators	[0-5] interval crossover, [1-30] mutation
Interval crossover parameter	[0.3 to 3]
Interval crossover not limited to interval	50%
Mutation frequency	[0.1 to 0.9]
Mutation standard deviation	[0.1 to 0.9]
A,B varies from	[-100 to -50] to [75 to 150]
p,q varies from	0 to [12 to 24]
C varies from	0 to [3 to 8]

Silicon Clusters

Table XXX

Conformation sets	30 "wall" dimers evenly spaced from 0.5-1.7. 70 "rest" dimers evenly space from 1.7-3.8 angstrom All other clusters including and randomized around the minimum energy (calculated with Menon's semi-empirical code) 67 3-atom clusters 51 4-atom clusters 41 5-atom clusters 34 6-atom clusters
Target energies generated by	SW with published parameters
Energy comparison	RMS of \|a - b\| / (\|a\| + \|b\|) on wall RMS elsewhere Each set of conformations generated a separate value and these were summed to get the fitness
Number of jobs	1001
Immigrants	25% jobs initial population started with best two-body evolved parameters. 25% jobs half of initial population started with best two-body evolved parameters

All other parameters were the same as for the Si-Si/Si-F/F-F studies.

Silicon Semi-Empirical Fitness Studies

Silicon Dimers

Table xxx lists the parameters used in the studies searching for only the Si two-body parameters using semi-empirical energies and forces in the fitness function.

Table xxx

Conformation sets

39 "far wall" dimers evenly spaced from 0.5 - 1.728 angstroms

7 "near wall" dimers evenly spaced from 1.599-1.793 angstroms

44 "minimum" dimers evenly spaced from 1.793 - 3.183 angstroms

41 "tail" dimers evenly spaced from 2.407 - 3.7 angstroms

All other clusters including and randomized around the minimum energy (calculated with semi-empirical code [reference])

67 3-atom clusters

51 4-atom clusters

41 5-atom clusters

34 6-atom clusters

Target energies generated by

Menon semi-empirical code

Energy and force comparisons

RMS of |a - b| / (|a| + |b|) on near and far wall

RMS on minimum

RMS of |a - b| / (|a| + |b|) on force for tail

Each set of conformations generated a separate value and these were summed to get the fitness. The near wall value was multiplied by 0.5 before the summation.

All other parameters were the same as the run searching for Si-Si two-body parameters with Stillinger-Weber published parameter generated energies.

Silicon Clusters

Table xxx lists the parameters used in the studies searching for all Si parameters using semi-empirical energies and forces in the fitness function.

Table xxx

Conformation sets

39 "far wall" dimers evenly spaced from 0.5 - 1.728 angstroms

7 "near wall" dimers evenly spaced from 1.599-1.793 angstroms

44 "minimum" dimers evenly spaced from 1.793 - 3.183 angstroms

41 "tail" dimers evenly spaced from 2.407 - 3.7 angstroms

Target energies generated by

Menon semi-empirical code

Energy and force comparisons

RMS of |a - b| / (|a| + |b|) on near and far wall

RMS on minimum and 3-6 atom clusters

RMS of |a - b| / (|a| + |b|) on force for tail

Each set of conformations generated a separate value and these were summed to get the fitness. The near wall value was multiplied by 0.5 before the summation.

All other parameters are the same as the Si cluster run with Stillinger-Weber published parameter energies in the fitness function.

Acknowledgments

We would like to thank NASA's NAS supercomputing facility for funding and computational support. Thanks to Eric Langhirt for maintaining the NAS Condor Pool and solving systems issues as they arose. We would also like to thank Charles Bauschlicher and Sandra Johan for assistance on parts of this project not described in this paper.

References

[Brenner 1990] Don W. Brenner, "Empirical Potential for Hydrocarbons for use in Simulating the Chemical Vapor Deposition of Diamond Films," Physical
Review B-Condensed Matter, 15 November 1990, V42 N15:9458-9471.

[Cundari and Fu 2000] T. R. Cundari, W. T. Fu, Inorganica Chemica Acta, "Genetic Algorithm Optimization of a Molecular Mechanics Force Field for Technetium," Inorganica Chimica Acta, 300302, pages 113-124, 2000.

[Drexler 1992] K. Eric Drexler, Nanosystems: Molecular Machinery, Manufacturing, and Computation, John Wiley & Sons, Inc..

[Globus, et. al. 1999] Al Globus, John Lawton, and Todd Wipke, "Automatic Molecular Design using Evolutionary Techniques," Nanotechnology, Volume 10, Number 3, September 1999, pages 290-299.

[Hunger, et. al. 1996] J. Hunger, S. Beyreuther and G. Huttner, “Modeling of tripod Metal Compounds RCH2C(CH2PR'R")3MLn: Optimization of Force Field Parameters by Genetic Algorithms,” Journal of Molecular Modeling 2, 257, 1996.

[Hunger, et. al. 1998] J. Hunger, S. Beyreuther, G. Huttner, K. Allinger, U. Radelof and L. Zsolnai, “How to Derive Force Field Parameters by Genetic Algorithms: Modelling tripod-Mo(CO)3 Compounds as an Example,” European Journal of Inorganic Chemistry, pages 693-702, 1998.

[Hunger and Huttner 1999] J. Hunger and G. Huttner, “Optimization and Analysis of Force Field Parameters by a Combination of Genetic Algorithms and Neural Networks,” Journal of Computational Chemistry, volume 20, pages 455-471, 1999.

[Litzkow, et al. 1988] M. Litzkow, M. Livny, and M. W. Mutka, "Condor - a Hunter of Idle Workstations,'' Proceedings of the 8th International
Conference of Distributed Computing Systems, pages 104-111, June 1988. See http://www.cs.wisc.edu/condor.

[Menon and Subbaswamy 1993] Madhu Menon and K. R. Subbaswamy, "Nonorthogonal Tight-Binding Molecular-Dynamics Study of Silicon Clusters," Physical Review B, Volume 47, Number 19, pages 754-759, 15 May 1993.

[Mohamadi, et. al. 1990] F. Mohamadi, N. G. J. Richards, W. C. Guida, R. Liskamp, M. Lipton, C. Caufield, G. Chang, T. Handrickson, W. C. Still, Journal of Computational Chemistry, volume 11, pages 440-467, 1990.

[Stillinger and Weber 1990] Frank H. Stillinger and Thomas A. Weber, “Dynamical Branching During Fluorination of the Dimerized Si(100) Surface: A Molecular Dynamic Study, Journal of Chemical Physics, 92(10), pages 6239-6245, 15 May 1990.

[Tersoff 1989] J. Tersoff, "Modeling Solid-State Chemistry: Interatomic Potentials for Multicomponent Systems," Physical Review B, volume 93, number 8, pages 5566-5568, 15 March 1989.