Crossover on Various Data Structures
Genetic algorithms seek to mimic natural evolution's ability to produce highly functional objects. Natural evolution produces organisms. Genetic algorithms produce sets of parameters, programs, molecular designs, and many other structures. Genetic algorithms usually solve problems by some variant of the following algorithm:
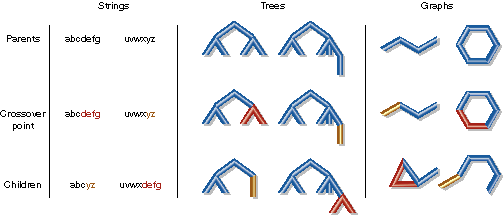
"The key point in deciding whether or not to use genetic algorithms for a particular problem centers around the question: what is the space to be searched? If that space is well-understood and contains structure that can be exploited by special-purpose search techniques, the use of genetic algorithms is generally computationally less efficient. If the space to be searched is not so well understood, and relatively unstructured, and if an effective GA representation of that space can be developed, then GAs provide a surprisingly powerful search technique for large, complex spaces." (italics added by [Forrest and Mitchell 1993])Genetic algorithms evolve populations by mutation and crossover. Graph mutation operators are fairly obvious and easy to implement. JavaGenes implements several graph mutation operators (add vertex, add edge, change vertex, change edge, etc.), but these are not the focus of this paper. Crossover is easy to implement for strings and trees because these data structures can be divided into two pieces at any point. Crossover applied to graphs is non-trivial.
Crossover on Various Data Structures

| Crossover can be applied to strings, trees, and graphs. Note that only graph crossover sometimes requires breaking multiple edges, and that fragment combination must work on fragments with different numbers of broken edges. |
For the purpose of our discussion, crossover may be considered to have two parts:
Our original motivation was to evolve molecules. At first, we attempted to devise a tree representation of molecules. However, many molecules contain cycles; which chemists call rings. Therefore, any attempt to use genetic programming to design molecules must have a mechanism to evolve cycles. This is non-trivial when crossover can replace any sub-tree with some other random sub-tree. After much thought, we were unable to devise a crossover-friendly tree representation of arbitrary cyclic graphs. Crossover-friendly means that any sub-tree is a potential crossover point without restriction.
Note that the problem we are solving here involves constructing graphs, rather than examining graphs. Many classic graph theoretical problems, graph coloring, finding Hamilton circuits, graph isomorphism, and maximal subgraphs discovery, have been studied in the computer science search literature. For example, see [Cheeseman, et al. 1991]. All of these problems investigate one or more graphs. Our problem is to find a graph representing a molecule or circuit with desirable properties. Thus, the characteristics of our search space are quite different from the classic graph problems in the literature. There is little or no reason to believe that crossover would be useful for solving these classic graph problems. It is possible to view the graph design problem as a search through the space of all possible graphs, and this space can be represented as an extremely large graph, as is explained in the next paragraph. However, rather than determining some property of the graph representing the search space, we simply look for one or more points in that space that possess desirable properties.
The space-of-all-graphs has very little in common with a multidimensional continuous Cartesian space. The space-of-all-graphs consists of a large number of discrete points, each of which represents a particular graph. One may define the neighbors of a graph to be all the graphs that could be formed by a single mutation. These mutations might be:
Circuit design is another field for which genetic algorithms using a graph representation should, in principle, be well suited. Genetic algorithms using a variable length string representation [Lohn and Colombano1998] and genetic programming [Koza 1997] [Koza 1999] have been used to design analog circuits. In the genetic programming case, a tree language capable of generating a subset of the analog circuits compatible with the SPICE (Simulation Program with Integrated Circuit Emphasis) simulator [Quarles, et al. 1994] was developed. The system was used to design a lowpass filter, a crossover filter, a four-way source identification circuit, a cube root circuit, a time-optimal controller circuit, a 100 dB amplifier, a temperature-sensing circuit, and a voltage reference source circuit. Thus, genetic algorithms can design graph-structured systems. Therefore, it may be advantageous to directly evolve graphs rather than strings or trees that are be interpreted to generate cyclic graphs.
[Nachbar 1998] used genetic programming to evolve molecules for drug design by sidestepping the crossover/cycles problem and representing molecules with trees. Each tree node represented an atom with bonds to the parent-node atom and each child-node atom. Hydrogen atoms were explicitly represented and are always leaf nodes. Rings were represented by numbering certain atoms and allowing a reference to that number to be a leaf node. Crossover was constrained not to break or form rings. Ring evolution was enabled by specific ring opening and closing mutation operators.
[Teller 1998] reported developing a graph crossover algorithm as part of his dissertation at Carnegie Mellon University, but supplied few details. This technique was applied to Neural Programming, a system developed by Teller to combine neural nets and genetic programming.
[Globus, et al. 1999] reported results evolving pharmaceutical drug molecules with the crossover operator discussed in this paper. The crossover operator was only capable of operating on undirected graphs, not the directed graphs required for circuits. Furthermore, after publication, a bug was discovered that severely limited cycle evolution. [Globus, et al. 1999] reported adequate performance evolving small molecules but poor results evolving larger molecules with more complex cycle structures; as might be expected in hindsight. The present paper reports results evolving the same molecules with the corrected operator as well as results on undirected graphs representing digital circuits. The molecular results are significantly better. See the Results section for details.
JavaGenes uses undirected graphs to represent molecules. Vertices are typed by atomic element. Edges can be single, double, or triple bonds. Valence is enforced. Heavy atoms (non-hydrogen atoms) are explicitly represented by vertices, but hydrogen atoms are implicit; i.e., any heavy atom with an unfilled valence is assumed to be bonded to hydrogen atoms, but these are not represented in the data structure. Since we're interested in the properties of the crossover operator, for this study JavaGenes evolved populations using crossover only and mutation was not used.
Each individual in the initial population was generated by the following algorithm:
The number of rings, by our definition, is always equal to bonds – atoms + 1. For this definition, single, double, and triple bonds are counted as one bond each. This formula corresponds to the following unambiguous definition of the rings in a molecule taken from [Corey and Wipke1969]. In this definition:
Tournament selection was used to choose parents in a steady state genetic algorithm. Tournament selection means that each parent is chosen by comparing two randomly chosen individuals and taking the best. Steady state means that new individuals (children) replace poor individuals in the population rather than creating a new generation. The poor individuals are also chosen by tournament, but the worst individual is selected for replacement. By convention, after population-size individuals have been replaced, we say that one generation is complete. The implementation follows this procedure:
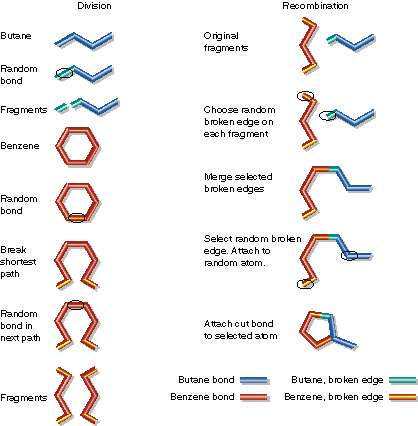
| Butane and benzene are divided at random points. Then a fragment of butane and a fragment of benzene are combined. Note that benzene must be cut in two places. Also, during fragment combination the benzene fragment has more than one broken edge. A random choice is made to connect this extra broken edge to a random atom in the butane fragment. Alternatively, the extra broken edge could have been discarded. |
Forming Fused Cycles and Cages with Crossover
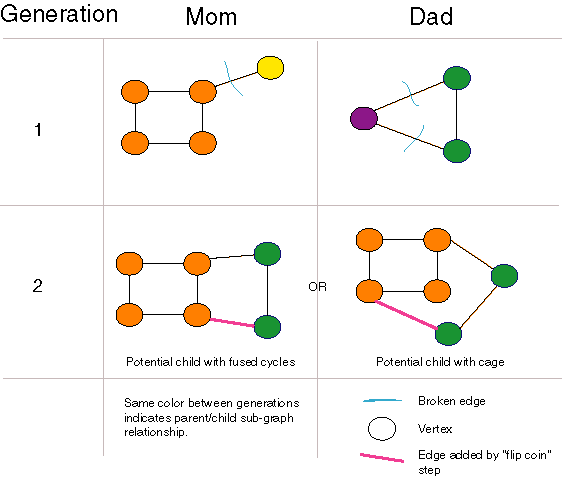
| Graph crossover can generate fused cycles and cages. The "flip coin" step of the crossover algorithm is crucial to this functionality. |
Our crossover operator can open and close rings using crossover alone, and can even generate cages and higher dimensional graph structures as long as there are rings in the population. Unfortunately, if there are no rings in a population, none can be generated. Also, once a population consists entirely of two-atom-molecules, no molecules with more than two atoms can be generated. Nonetheless, this crossover operator is the most general of those we examined or found in the literature. In particular, unlike [Nachbar 1998], no special-purpose ring opening and closing operators are necessary. Unlike [Weininger 1995], no parameters are necessary and disconnected "molecules" are never produced.
The computational resources required for genetic algorithms to find a solution is a function of the size of the search space, among other factors. The space of all possible graphs is combinatorial and enormous. For molecular design, this space can be radically reduced by enforcing valence limits for each atom. Thus, a carbon atom with one double and two single bonds will not be allowed to add another bond. Also, avoiding explicit representation of hydrogen atoms substantially reduces the size of the graph.
JavaGenes uses directed cyclic graphs to represent circuits. In other words, each vertex has a set of input edges and a set of output edges, and each edge has an input vertex and an output vertex. Each vertex and edge has a current state (usually 0 or 1). Vertices are the digital devices And, Nand, Or, Nor, Xor, and Nxor. The initial value of a device may be zero or 1. Each device can have any number (including zero) of input and output edges. If there are no input edges, And, Or, and Xor output 0, and Nand, Nor, and Nxor output 1. If there is one input edge, it is copied to output or inverted for Nand, Nor, and Nxor vertices. If there are two or more input edges:
There are two special vertices in each circuit: input and output. The input vertex does no processing, but simply accepts values from a simulator and outputs those values to all output edges. No input edges are allowed. The output vertex is a digital device like the others, but has no output edges. The output vertex hands output values to a simulator.
Each individual in the initial population was generated by choosing a random number of vertices and edges where the numbers fell within upper and lower bounds set by the JavaGenes input parameters. Vertex types were randomly chosen from all possible types. The circuits were created as follows:
This modified crossover operator has the interesting property that, under certain rare conditions, a disconnected circuit can be created. This anomaly requires multiple generations to occur, and is caused by the fact that the edges are directed. While we have not collected data, the anomaly appears to occur only once for every few thousand crossover operations. When this occured, we simply discarded the child.
Evolving a Disconnected Circuit
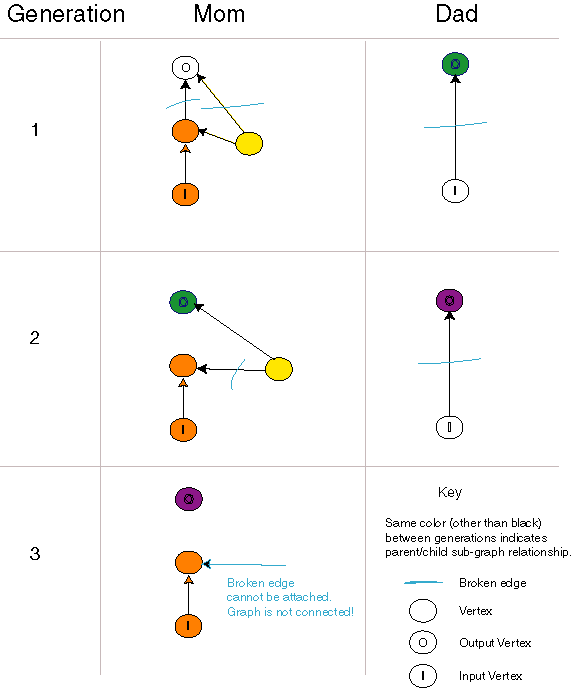
| This sequence of evolutionary events results in a disconnected directed graph. Fortunately, this occurs rarely. The key event comes in the second generation when the left-hand individual is broken into fragments. One fragment contains an input vertex and a single broken edge that can only be attached to an output edge of a vertex. Such a fragment can rarely be attached to a fragment containing an output vertex. |
where c is the candidate's bag and t is the target's bag. Two elements are considered identical for the purpose of the intersection and union operators if the atoms have the same extended types and the distance between them is identical. Each duplicate in the bag is considered a separate element for the purpose of the intersection and union operators. The Tanimoto index always returns a number between 0 and 1. We prefer fitness functions that return lower numbers for fitter individuals, so we subtract the Tanimoto index from one to get the fitness.Search spaces with many local optima are difficult to examine because many algorithms tend to converge to local optima and miss the global optimum. The all-pairs-shortest-path fitness function has many local optima over the space-of-all-molecules whenever the target molecule contains rings. Consider benzene, a six membered ring, as the target molecule. Any ring other than a six membered ring will be at a local optima because a bond must be removed, lowering the fitness in most cases, before bonds and atoms can be added to generate benzene. Thus, any target molecule containing rings will have an associated search space containing many local optima. Interestingly, a small modification in the definition of the space-of-all-molecules eliminates these local optima. Consider mutations that
The targets for this study were benzene, cubane, purine, diazepam, morphine and cholesterol. All targets contain rings and thus generate a search space with local optima. The fitness function can not only find similar molecules, which is useful in drug design, but can also lead evolution to the exact molecule used as the target. This can prove that the algorithm can find particular molecules. In addition, the number of generations to find the target provides a crude quantitative measure of performance.
Some initial runs ran out of memory when the circuits became extremely large. To reward parsimony, a fitness penalty of one percent was assessed against a circuit for each additional edge or vertex the circuit grew above a certain size. The penalty-free size was chosen to be well above that necessary to create the circuit.
JavaGenes is implemented in Java. Java was chosen because its syntax is similar to C++, many useful libraries are available (the graph layout software [Tunkelang 1998] and some statistics code were contributed by others), garbage collection vastly simplifies memory management, and Java’s array bounds checking and other bug-limiting features seem to substantially reduce debugging time and produce more robust code than C++, Fortran or C. A run-time penalty is paid for these advantages, but a generation of 500 individuals typically takes less than a minute to compute. The only significant performance problem has been with Java serialization. JavaGenes used serialization to checkpoint. Serialization is the process of flattening a data structure into an array of bytes, a form that can be saved to disk. Serialization is a standard part of the Java language. Although standard Java serialization worked well for small data structures, when the data structures grew large, serialization could take hours. Standard Java serialization was replaced with custom checkpoint/restart code, reducing checkpoint/restart time to around 10 seconds in most cases with a maximum around five minutes. See [Globus, et al. 2000] for a more detailed investigation of this problem.
Long serialization times created a serious problem. In the initial implementation, JavaGenes started a new random number generator after restart. Because of this, evolution did not follow the same path taken after the last checkpoint. The genetic algorithm was controlled by different random numbers and therefore searched a different part of the space-of-all-graphs. Because the number of generations to find a specific target was used as the performance measure, re-starting the search repeatedly after a checkpoint made the algorithm appear more efficient than it was. Consider the case where a job ran for 100 generations up to a checkpoint and 20 more generations before being killed. When the job was restarted, a different set of populations would be constructed and one of the new generations, say the 10th, might find the target. Therefore, it would appear as if the target was found in 110 generations, but actually 130 populations were generated. Thus, when checkpoint times were long compared to the time available for execution on a single workstation, jobs might repeatedly search the region around the last checkpoint and stop if a solution were found, reporting an inaccurately small number of generations to completion. It was therefore necessary, at job restart time, to restart the random number generator with the same seed and then execute the random number generator until the sequence was where it left off. This should have insured that jobs followed the same evolutionary path regardless of checkpoint history. Unfortunately, although this fix worked properly when a job was restarted on the same machine, different results were observed in normal execution on the Condor pool, where jobs frequently move between machines. The changing evolutionary path was presumably caused by differences in the Java libraries on different versions of the SGI operating system. This may change the order of certain lists in JavaGenes and cause the same random number to pick a different item from a list. While this problem may make the results reported below somewhat optimistic for the larger molecules and circuits, we believe that the effect is fairly minor now that checkpointing is fast. There should be little effect on the smaller molecules because most jobs completed before the first checkpoint. Because checkpointing was fast, computations would usually proceed to the next checkpoint before being stopped and restarted. Only ~6% of all generations were repeated once the checkpointing performance problem was corrected.
There was an additional problem during circuit evolution that was also caused by checkpointing. Each time a job restarted, a different set of random binary inputs was chosen to evaluate candidate circuits. This could have the effect of changing the fitness of a given circuit, although usually the change would be minor if the input sequence was long. Nonetheless, individuals generated after a restart could find themselves with a lower or higher fitness with respect to an older individual than if the restart had not taken place. We do not believe that this had any significant effect on the results.
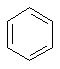 benzene
(C6H6) a simple ring molecule.
benzene
(C6H6) a simple ring molecule.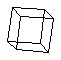 cubane (C8H8)
a cage molecule.
cubane (C8H8)
a cage molecule.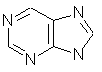 purine (C5H4N4)
fused rings and heteroatoms.
purine (C5H4N4)
fused rings and heteroatoms.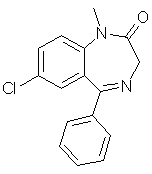 diazepam (C16H13ClN2O)
used in [Carhart, et al. 1985].
diazepam (C16H13ClN2O)
used in [Carhart, et al. 1985].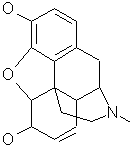 morphine (C17H19NO3)
Dr. Wipke's group has worked on morphine analog design for many years.
morphine (C17H19NO3)
Dr. Wipke's group has worked on morphine analog design for many years.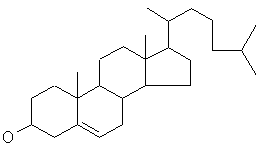 cholesterol
(C27H46O) a non-drug molecule.
cholesterol
(C27H46O) a non-drug molecule. 1-bit add. Note that this circuit
wouldn't work in hardware, but because our simulator assumes unit propagation
delays for every device and wire, the simulated circuit will perform
properly.
1-bit add. Note that this circuit
wouldn't work in hardware, but because our simulator assumes unit propagation
delays for every device and wire, the simulated circuit will perform
properly.Finding Benzene, Cubane, and Purine
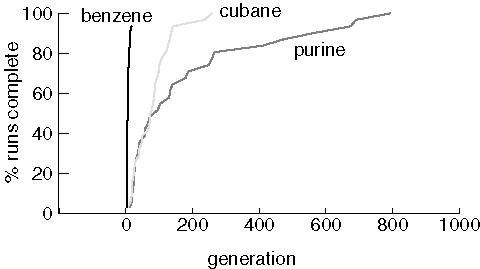
Note that two benzene jobs did not find the target at all, even though benzene was usually found in just a few generations. The runs that could not find benzene lost all of the cycles in the population in the first generation created by crossover. When a population consists entirely of non-cyclic molecules, the crossover operator can not generate cycles.
Finding Diazepam, Morphine, and Cholesterol
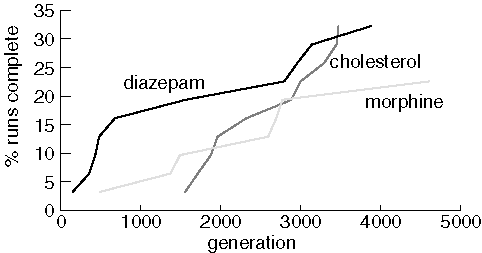
Although each run consisted of 31 jobs, only ten runs found diazepam and cholesterol, and only seven runs found morphine. Note that JavaGenes performance is much poorer on these larger molecules. Presumably, this is because the size of the space-of-all-molecules explodes combinatorially as molecule size increases. We also noticed that some populations lost all of the rare elements in the target. For example, diazepam has only one chlorine and one oxygen atom. Several of the diazepam jobs lost all of one these elements from the population and were forever doomed. Interestingly, runs that lost all oxygen and/or chlorine from the population did so within about 400 generations. Using vertex mutation should avoid this situation, but this paper is concerned with the properties of the crossover operator.
Now we examine JavaGenes performance searching for the same three molecules using a population of 1,000 and a maximum of 10,000 generations.
Finding Larger Molecules with a Larger Population
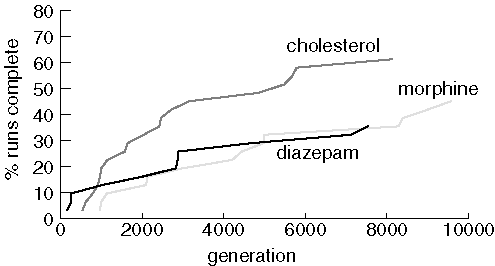
Performance is improved with a larger population and more generations, but 20 runs still failed to find diazepam, 17 couldn't find morphine, and 12 failed to find cholesterol.
Finding Purine With Different Population Sizes
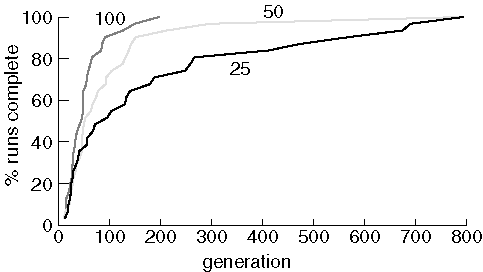
As expected, increasing the population size improves performace. Interestingly, with a population size of 25 and 50, the last job to find the target molecule took about the same number of generations. This is probably a random event, suitable for publication in the Journal of Irreproducable Results.
Identical Experiments Finding Purine
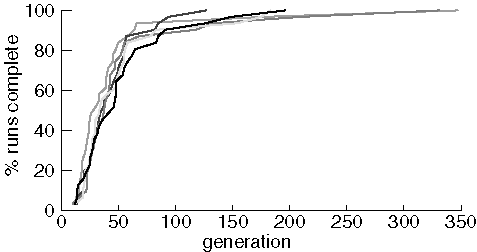
The variability between experiments is quite small for this molcular target. Most of the difference appears in the last two or three runs to find purine from each experiment. To see if variablity was different with a more difficult target, we compare two experiments searching for diazepam using a population size of 500 and a maximum of 5,000 generations:
Identical Experiments Finding Diazepam
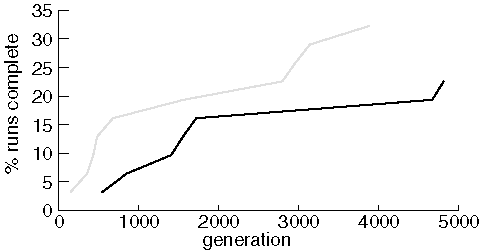
Note that although each run consisted of 31 jobs, only 7 and 10 runs, respectively, were able to find diazepam in 5,000 generations. Nonetheless, although one experiment clearly out-performed the other, the results of the two experiments are roughly comparable.
Finding Circuits
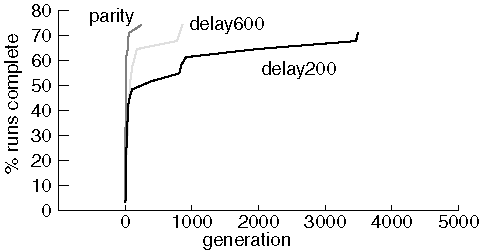
Note that only 22-24 (out of 31) runs succeeded in finding a proper circuit in each experiment. Results are very similar for most of the successful runs with substantial variability only for the worst performing runs that succeeded. In spite of many attempts, we were never able to evolve a perfect 1-bit add circuit. The source of the problem is unclear, although it may be that the crossover operator does not preserve useful sub-graphs very often.
31 Runs Searching for Morphine
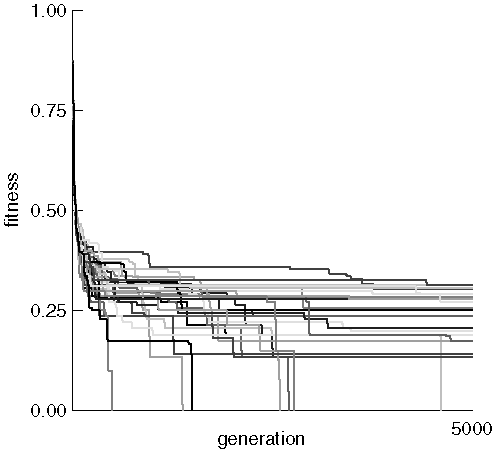
The initial random populations all had a best individual fitness near 0.9, but quickly inproved to around 0.25. Most runs then leveled off with long periods of no improvement, occasionally punctuated by sudden bursts of increasing fitness. Notice that morphine was often found even when the previous best fitness was quite poor, as evidenced by the long verticle lines ending at the x-axis. This indicates that fitness improved very rapidly over the course of a few tens of generations.
We now examine the mean fitness of each run in the same experiment:
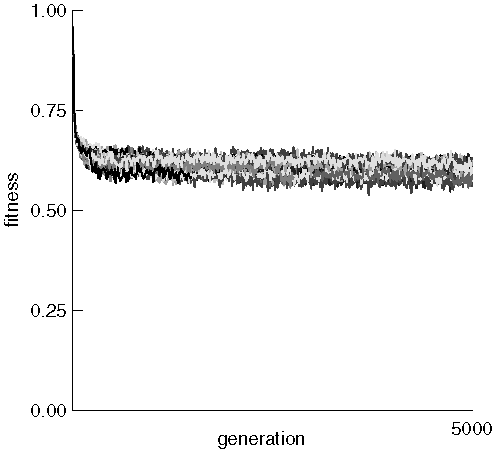
The mean fitness of each run dropped rapidly from about 0.96 to somewhere near 0.6 and stayed there with only very minor improvement. This may be caused by the extremely destructive nature of the crossover operator, which can be expected to generate many very unfit children from fit parents. Eery generated child was placed back into the fixed-size population, and there was no guarantee that the individual replaced had lower fitness than the child. It might be interesting to develop a procedure that rarely replaces individuals if the child has worse fitness. One might expect the average fitness to continue to improve as evolution proceeds.
Table 1: Finding Small Molecules With and (Without) "Coin Flip" Step
| 31 runs for
each molecule (20 with bug) |
Population size | Median generations to find target | Minimum generations to find target | Number of runs that failed to find target |
Maximum generations
|
| Benzene |
100 (200)
|
3 (39.5)
|
0 (2)
|
0 (8)
|
10 (1000)
|
| Cubane |
100
|
20 (46.5)
|
4 (13)
|
0 (0)
|
140(NR)
|
| Purine |
100
|
38 (245)
|
6 (19)
|
0 (4)
|
269(1000)
|
NR = not recorded. Because of run-to-run variability, and because many runs did not complete, median, rather than mean, generations to find the target is used, a procedure suggested by [Claerbout and Muir 1973].
Diazepam, morphine, and cholesterol were never found more than once each in [Globus, et al. 1999]. The difference in results before and after the bug fix show the importance of the "flip coin" step.
Comparison With Random Search
| case | number of runs that found purine | median generations to find purine |
| random search |
0
|
N/A
|
| crossover alone |
21
|
37
|
| 50-50 mix of crossover and random search |
21
|
48
|
Clearly the crossover operator is better than random search.
JavaGenes can clearly find molecules and simple circuits. The algorithm consistently finds molecules but has great difficulty with circuits. Even the simple delay and parity circuits were not always found.
Chemists have known for over a century that graphs are the most natural representation for molecules, just as logic designers use graphs to represent circuits. Furthermore, the space-of-all-graphs is not well understood or characterized. Therefore, it is reasonable to presume that searching for graphs using genetic algorithms will be profitable in a number of domains. We hope that our crossover operator will make a contribution.
[Carhart, et al. 1985] Raymond Carhart, Dennis H. Smith, and R. Venkataraghavan, "Atom Pairs as Molecular Features in Structure-Activity Studies: Definition and Application," Journal of Chemical Information and Computer Science, volume 23, pages 64-73.
[Cheeseman, et al. 1991] Peter Cheeseman, Bob Kanefsky, William M. Taylor, "Where the Really Hard Problems Are," Proceedings of the 12th International Conference on Artificial Intelligence, Darling Harbor, Sydney, Australia, 24-30 August 1991.
[Claerbout and Muir 1973] J. F. Claerbout and F. Muir, ``Robust Modeling with Erratic Data,'' Geophysics, volume 38, pages 826-844.
[Corey and Wipke 1969] E. J. Corey and W. Todd Wipke, "Computer-Assisted Design of Complex Organic Syntheses," Science, volume 166, pages 178-192, 10 October 1969.
[De Jong 1990] K. A. De Jong "Introduction to the Second Special Issue on Genetic Algorithms," Machine Learning, 5 (4), 1990.
[Forrest and Mitchell 1993] Stephanie Forrest and Melanie Mitchell, "What Makes a Problem Hard for Genetic Algorithm? Some Anomalous Results in the Explanation," Machine Learning, volume 13, pages 285-319.
[Globus, et al. 1999] Al Globus, John Lawton, and Todd Wipke, "Automatic Molecular Design Using Evolutionary Techniques," Nanotechnology, volume 10, number 3, September 1999, pages 290-299.
[Globus, et al 2000] Al Globus, Eric Langhirt, Miron Livny, Ravishankar Ramamurthy, Marvin Solomon, Steve Traugott, "JavaGenes and Condor: Cycle-Scavenging Genetic Algorithms," Java Grande 2000, sponsored by ACM SIGPLAN, San Francisco, California, 3-4 June 2000.
[Holland 1975] John H. Holland, Adaptation in Natural and Artificial Systems, University of Michigan Press.
[Kinnear 1994] Kenneth E. Kinnear, Jr., "A Perspective on the Work in this Book," Advances in Genetic Programming, edited by Kenneth E. Kinnear, Jr., MIT Press, Cambridge, Massachusetts, pages 3-20, 1994.
[Koza 1992] John R. Koza, Genetic Programming: on the Programming of Computers by Means of Natural Selection, MIT Press, Massachusetts, 1992.
[Koza, et al. 1997] John R. Koza, Forrest H. Bennett III, David Andre, Martin A. Keane and Frank Dunlap, "Automated Synthesis of Analog Electrical Circuits by Means of Genetic Programming," IEEE Transactions on Evolutionary Computation, volume 1, number 2, pages 109-128, July 1997.
[Koza, et al. 1999] John R. Koza, Forrest H. Bennett, Martin A. Keane, Genetic Programming III : Darwinian Invention and Problem Solving, Morgan Kaufmann Publishers, ISBN: 1558605436.
[Litzkow, et al. 1988] M. Litzkow, M. Livny, and M. W. Mutka, "Condor - a Hunter of Idle Workstations,'' Proceedings of the 8th International Conference of Distributed Computing Systems, pp. 104-111, June1988. See http://www.cs.wisc.edu/condor/.
[Lohn and Colombano 1998] Jason D. Lohn and Silvano P. Colombano, "Automated Analog Circuit Synthesis Using a Linear Representation,'' Second International Conference on Evolvable Systems: From Biology to Hardware, Springer-Verlag, 23-25 September 1998.
[Nachbar 1998] Robert B. Nachbar, "Molecular evolution: a Hierarchical Representation for Chemical Topology and its Automated Manipulation," Proceedings of the Third Annual Genetic Programming Conference, University of Wisconsin, Madison, Wisconsin, 22-25 July 1998, pages 246-253.
[Quarles, et al. 1994] T. Quarles, A. R. Newton, D. O. Pederson, and A. Sangiovanni-Vincentelli, SPICE 3 Version 3F5 User's Manual, Department of Electrical Engineering and Computer Science, University of California at Berkeley, CA, March 1994.
[Teller 1998] Astro Teller, "Algorithm Evolution with Internal Reinforcement for Signal Understanding," Computer Science PhD Thesis, Carnegie Mellon University, Publication Number: CMU-CS-98-132.
[Tunkelang 1998] Daniel Tunkelang, A Numerical Optimization Approach to Graph Drawing, Dissertation, Carnegie Mellon University, School of Computer Science, December 1998.
[Weininger 1995] David Weininger, "Method and Apparatus for Designing
Molecules with Desired Properties by Evolving Successive Populations,"
U.S. patent US5434796, Daylight Chemical Information Systems, Inc.