Graph Crossover
Al Globus, CSC at NASA Ames Research Center
Sean Atsatt, Sierra Imaging, Inc.
John Lawton, University of California at Santa Cruz
Todd Wipke, University of California at Santa Cruz
Abstract
Most genetic algorithms use string or tree representations. To apply genetic
algorithms to graphs, a good crossover operator is necessary. We have developed
a general-purpose, novel crossover operator for directed and undirected
graphs, and used this operator to evolve molecules and circuits. Unlike
strings or trees, a single point in the representation cannot divide every
possible graph into two parts, because graphs may contain cycles. Thus,
the crossover operator is non-trivial. A steady-state, tournament selection
genetic algorithm code (JavaGenes) was used test the graph crossover operator.
JavaGenes has successfully evolved pharmaceutical drug molecules and simple
digital circuits. For example, morphine, cholesterol, and diazepam were
successfully evolved by 30-60% of runs within 10,000 generations using
a population of 1000 molecules. Since representation strongly affects genetic
algorithm performance, adding graphs to the evolutionary programmer's bag-of-tricks
should be beneficial. Also, since graph evolution operates directly on
the phenotype, genotype to phenotype decoding is eliminated.
Introduction
Genetic algorithms have been usefully applied to two data structures, strings
and trees. One might ask: "Can the same techniques may be usefully extended
to other data structures; for example, graphs?" Graph mutation operators
are fairly obvious and easy to implement. JavaGenes implements several
graph mutation operators (add vertex, add edge, change vertex, change edge,
etc.), but these are not the focus of this paper. Crossover is easy to
implement for strings and trees because these data structures can be divided
into two pieces at any point. Graph crossover can be accomplished by breaking
edges. However, graph crossover is complex because:
-
Graph crossover cannot trivially divide the data structure at any point,
because any edge may be a member of one or more cycles. All
of these cycles may need to be broken to divide the graph into two pieces
if the edges to break are chosen at random to avoid biasing the search.
One cannot avoid breaking edges involved in cycles, because then the cycle
structure will not evolve.
-
Graph fragments produced by division may have more than one crossover point
("broken edges") that requires reattachment during fragment combination.
-
When two fragments are combined they may have different numbers of
broken edges to be merged.
-
For a graph crossover operator to potentially reach any possible graph
from an initial random population, the crossover operator must be able
to create and destroy individual cycles, fused cycles (cycles that share
edges), cages (two or more cycles, each pair of which share at least two
edges), and combinations of fused cycles and cages.
The primary contribution of this paper is to introduce a new graph crossover
operator that:
-
Can operate on any connected directed or undirected graph. A connected
graph is one where every pair of vertices is connected by at least one
set of edges.
-
Divides graphs at randomly generated cut sets. A cut set is a set of edges
which divides a connected graph into two parts.
-
Can evolve arbitrary cyclic structures given at least some cycles in the
initial population.
-
Always produces connected undirected graphs.
-
Almost always produces connected directed graphs.
Our graph crossover operator was applied to evolving pharmaceutical drug
molecules and simple digital circuits. Molecules were represented as a
set of atoms (vertices) connected by a set of bonds (edges). Digital circuits
were represented as a set of devices (vertices) connected by a set of wires
(edges). Tree representations have been used to evolve molecules and circuits.
However, many molecules and circuits contain cycles; which chemists call
rings. Therefore, any attempt to use genetic programming to design molecules
and circuits must have a mechanism to evolve cycles. This is non-trivial
when crossover can replace any sub-tree with some other random sub-tree.
Previous work as either limited the class of cyclic structures that can
be evolved or used mutation to evolve cycles.
Previous work
[Weininger 1995] patented genetic algorithms for molecular design, and
used the standard graph representation of a molecule in the crossover operator.
The patent describes the straightforward and obvious parts of mapping genetic
algorithm techniques to graph-based molecular design, and the non-obvious
portions: the crossover algorithm and fitness functions. The crossover
algorithm described in the patent depends on two parameters: a digestion
rate, which breaks bonds, and a dominance rate, which controls how many
parts of each parent appear in a child. As described by the text and figure
7 in the patent, [Weininger 1995]'s crossover algorithm removes random
bonds from parents according a "digestion rate" to create fragments, and
does not connect the fragments from both parents with new bonds
when forming children. A "dominance rate" determines how many fragments
of each parent are placed in the child, which can obviously lead to disconnected
children. When restricted to generating connected children (covalently
bound molecules), [Weininger 1995]'s crossover operator generates a child
that is simply a fragment of one parent, so in this case the operation
is not really crossover at all, but rather a form of mutation. [Weininger
1995] uses the Tanimoto index (described below)
as a distance measure for a number of fitness functions. Daylight Chemical
Information Systems, Inc., which holds the patent, reports using genetic
algorithm techniques to discover lead compounds for pharmaceutical drug
development and other commercial successes.
Circuit design is another field for which genetic algorithms using a
graph representation should, in principle, be well suited. Genetic algorithms
using a variable length string representation [Lohn and Colombano1998]
and a tree representation [Koza 1997] [Koza 1999] have been used to design
analog circuits. In each case, a language capable of generating a subset
of the analog circuits compatible with the SPICE (Simulation Program with
Integrated Circuit Emphasis) simulator [Quarles, et al. 1994] was developed.
In particular, the class of cycles that can be generated is limited. The
tree representation was used to design a lowpass filter, a crossover filter,
a four-way source identification circuit, a cube root circuit, a time-optimal
controller circuit, a 100 dB amplifier, a temperature-sensing circuit,
and a voltage reference source circuit. Thus, genetic algorithms can design
graph-structured systems, albeit with some limitations.
[Nachbar 1998] used genetic programming to evolve molecules for drug
design by sidestepping the crossover/cycles problem and representing molecules
with trees. Each tree node represented an atom with bonds to the parent-node
atom and each child-node atom. Hydrogen atoms were explicitly represented
and were always leaf nodes. Rings were represented by numbering certain
atoms and allowing a reference to that number to be a leaf node. Crossover
was constrained not to break or form rings. Ring evolution was enabled
by specific ring opening and closing mutation operators.
[Teller 1998] reported developing a graph crossover algorithm as part
of his dissertation at Carnegie Mellon University, but supplied few details.
This technique was applied to Neural Programming, a system developed by
Teller to combine neural nets and genetic programming.
[Globus, et al. 1999] reported results evolving pharmaceutical drug
molecules with the crossover operator discussed in this paper. The crossover
operator was only capable of operating on undirected graphs, not the directed
graphs required for circuits. Furthermore, after publication, a bug was
discovered that severely limited cycle evolution. [Globus, et al. 1999]
reported adequate performance evolving small molecules but poor results
evolving larger molecules with more complex cycle structures; as might
be expected in hindsight. The present paper reports results evolving the
same molecules with the corrected operator as well as results on undirected
graphs representing digital circuits. The molecular results are significantly
better. See the
Results section for details.
Method
Genetic Algorithm with Graph Representation
Molecules
One approach to drug design is to find molecules similar to good drugs.
Ideally, a candidate replacement drug is sufficiently similar to have the
same beneficial effect, but is different enough to avoid negative side
effects. To use genetic algorithms for similarity-based drug discovery,
we need a good similarity measure that can score any molecule. [Carhart,
et al. 1985] defined such a similarity measure, all-atom-pairs-shortest-path,
and searched a large database for molecules similar to diazepam. We used
this similarity measure to evolve a population of molecules towards a target
molecule.
JavaGenes uses undirected graphs to represent molecules. Vertices are
typed by atomic element. Edges can be single, double, or triple bonds.
Valence is enforced. Heavy atoms (non-hydrogen atoms) are explicitly represented
by vertices, but hydrogen atoms are implicit; i.e., any heavy atom with
an unfilled valence is assumed to be bonded to hydrogen atoms, but these
are not represented in the data structure. Enforcing valence and ignoring
hydrogen reduces the size of the search space.
Each individual in the initial population was generated by the following
algorithm:
-
atoms = random number between half and twice the number in the target molecule
-
rings = random number between half and twice the number in the target molecule
-
while (true)
-
for some number of tries
-
choose first atom at random
-
for atoms-1
-
if possible, add random atom bonded (with random bond) to a random existing
atom, respecting valence
-
for number of rings
-
if possible, add random bond between two randomly chosen atoms, respecting
valence
-
if molecule has correct number of atoms and rings, return molecule
-
rings--
The random atoms were chosen with equal probability from the elements in
the target molecule. Thus, the initial population of a run searching for
cholesterol would have roughly equal numbers of carbon and oxygen atoms.
The random bonds (single, double, or triple) were chosen with equal probability
from the bond types in the target molecule. The last step (rings--) is
necessary because it is possible to run out of empty valence before molecular
construction is complete. Consider the case where the first atom is chlorine.
If the second atom is also chlorine, the two chlorine atoms must share
a single bond and the valence of both atoms will be filled, so no additional
atoms may be added. If the random generation algorithm fails to make a
molecule with the proper number of atoms and rings, then the algorithm
tries again. Some choices of "atoms" and "rings" require a molecule with
more rings than is possible given the number of atoms. Consider searching
for cubane. If atoms = 4 and rings = 16, it is impossible to build a molecule
that matches the specification. Therefore, after trying to generate a molecule
several times, the algorithm will reduce the number of required rings by
one and try again. Since all of the target molecules contain at least one
element with a valence of two or more, there is no hard limit to the number
of atoms that may be in a molecule.
The number of rings, by our definition, is always equal to bonds
– atoms + 1. For this definition, single, double, and triple
bonds are counted as one bond each. This formula corresponds to the following
unambiguous definition of the rings in a molecule taken from [Corey and
Wipke1969]. In this definition:
-
the set of all rings must include all the bonds participating in any ring,
-
removing any ring will result in at least one bond not being included in
any ring,
-
no ring may share more than half its bonds with any other ring,
-
and the set of rings chosen must be at least as large as any other set
of rings with the first three properties.
While this definition is precise and easy to code, it comes to the interesting
conclusion that cubane (a cubic molecule) has five rings, not six. Consider
the six sides of cubane to be the six rings in the set of rings.
If any one of the six rings is removed from the set of rings, all bonds
are still included in the set of rings violating property #2. Therefore,
only five rings are necessary to meet the definition.
Tournament selection was used to choose parents for a steady state genetic
algorithm. Individuals to replace were also chosen by tournament, but the
worst individual was selected for replacement. By convention, after population-size
individuals have been replaced, we say that one generation is complete.
Since we're interested in the properties of the crossover operator, for
this study JavaGenes evolved populations using crossover only with no mutation.
To divide a molecule into two fragments we use the following procedure:
-
Choose an initial random bond
-
Repeat
-
Find the shortest path between the initial bond's vertices (the first
time this will simply be the initial bond).
-
Remove and remember a random bond from this path. These bonds are called
"broken edges."
-
Until a cut set is found, i.e., no path exists between the initial
bond's vertices.
To combine fragments we use the following procedure:
-
Repeat
-
Select a random broken edge. Determine which fragment it is associated
with.
-
If at least one broken edge in other fragment exists
-
choose one at random
-
merge the broken edges into one bond; respecting valence by reducing
the order of the bond if necessary
-
Else flip coin (this step was disabled by a bug in [Globus, et al.
1999])
-
if heads -- attach the broken edge to a random atom in other fragment
(respecting valence)
-
if tails -- discard the broken edge
-
Until each broken edge has been processed exactly once
Graph Crossover of Butane and Benzene to Create a Child
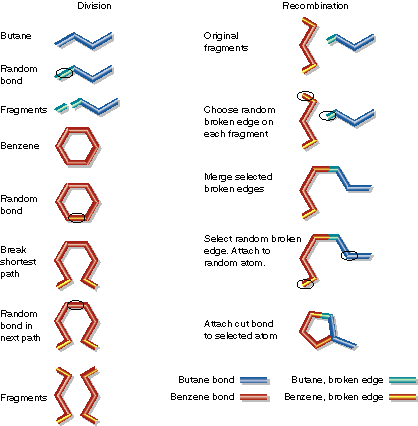
| Butane and benzene are divided at random points. Then
a fragment of butane and a fragment of benzene are combined. Note
that benzene must be cut in two places. Also, during fragment combination
the benzene fragment has more than one broken edge. A random choice is
made to connect this extra broken edge to a random atom in the butane fragment.
Alternatively, the extra broken edge could have been discarded. |
Forming Fused Cycles and Cages with Crossover
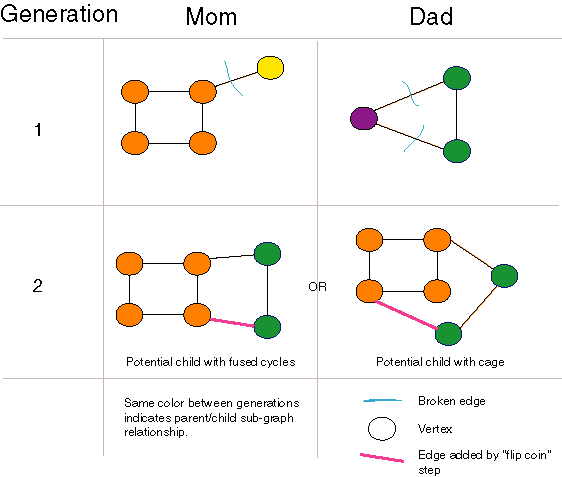
| Graph crossover can generate fused cycles and cages.
The "flip coin" step of the crossover algorithm is crucial to this functionality. |
Our crossover operator can open and close rings using crossover alone,
and can even generate cages and higher dimensional graph structures as
long as there are rings in the population. If there are no rings in a population,
none can be generated. Also, once a population consists entirely of two-atom
molecules, no molecules with more than two atoms can be generated. Nonetheless,
this crossover operator is the most general of those we examined or found
in the literature. In particular, unlike [Nachbar 1998], no special-purpose
ring opening and closing operators are necessary. Unlike [Weininger 1995],
no parameters are necessary and disconnected "molecules" are never produced.
Digital Logic
JavaGenes uses directed cyclic graphs to represent circuits. In other words,
each vertex has a set of input edges and a set of output edges, and each
edge has an input vertex and an output vertex. Each vertex and edge has
a current state (usually 0 or 1). Vertices are the digital devices And,
Nand, Or, Nor, Xor, and Nxor. The initial value of a device may be 0 or
1. The initial value of wires is X (unknown). Each device can have any
number (including zero) of input and output edges. If there are no
input edges, And, Or, and Xor output 0, and Nand, Nor, and Nxor output
1. If there is one input edge, it is copied to output or inverted for Nand,
Nor, and Nxor vertices. If there are two or more input edges:
-
And will output 0 if any input value is 0, or 1 if all input values are
1.
-
Or will output 0 if all input values are 0, or 1 if any input value is
1.
-
Xor will output 0 if an even number of input values are 1, or 1 if an odd
number of input values are 1.
For the devices whose names start with N and have two or more input edges,
the output is inverted (0 becames 1, 1 becomes 0). This scheme allows vertices
to have any number of input and output edges, thereby simplifying the crossover
operator substantially. Any circuit represented this way can be easily
mapped to a circuit restricted to two and three terminal devices plus fan
out.
There are two special vertices in each circuit: input and output. The
input vertex does no processing, but simply accepts values from a simulator
and outputs those values to all output edges. No input edges are allowed.
The output vertex is a digital device like the others, but has no output
edges. The output vertex hands output values to a simulator.
Each individual in the initial population was generated by choosing
a random number of vertices and edges where the numbers fell within upper
and lower bounds set by input parameters. Vertex types were randomly chosen
from all possible types. The circuits were created as follows:
-
Input and output vertices were created
-
The rest of the vertices were added one at a time by attaching one output
edge to the input of a vertex already in the circuit.
-
An output edge from the input vertex was connected to a random vertex.
-
Edges were added at random to create the required number of cycles.
Because edges were directed and there were two special vertices in each
circuit (the input and output vertices), the crossover algorithm was somewhat
different than for molecules. During division, instead of choosing a random
edge and cutting random edges from paths connecting the vertices of the
chosen edge, the input and output vertices were chosen and edges on paths
between them were broken until the graph divided into two parts.
This guaranteed that each fragment had exactly one input or one output
vertex, but never both. Obviously, only fragments containing an input vertex
were combined with fragments containing an output vertex, and vice versa.
Furthermore, during combination, broken edges with the output vertex removed
were only merged with broken edges where the input vertex was removed,
and vice versa.
This modified crossover operator has the interesting property that,
under certain rare conditions, a disconnected circuit can be created. This
anomaly requires multiple generations to occur, and is caused by the fact
that the edges are directed. While we have not collected data, the anomaly
appears to occur only once every few thousand crossover operations. When
this occured, we simply discarded the child.
Evolving a Disconnected Circuit
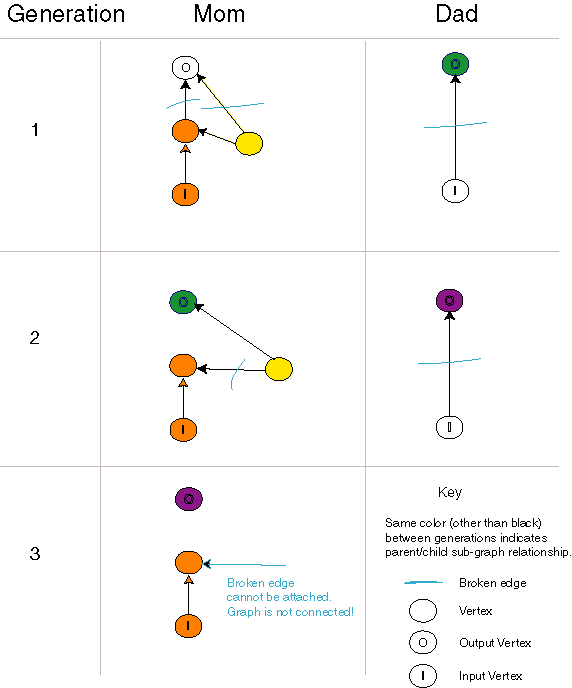
| This sequence of evolutionary events results in a disconnected
directed graph. Fortunately, this occurs rarely. The key event comes in
the second generation when the left-hand individual is broken into fragments.
One fragment contains an input vertex and a single broken edge that can
only be attached to an output edge of a vertex. Such a fragment can not
always be attached to a fragment containing an output vertex. |
Fitness Functions
Molecules: all-pairs-shortest-path similarity
For our initial studies we wanted a fitness function that only required
the graph of a molecule, not the xyz coordinates of each atom.This simplified
initial studies and avoided minimizing the energy of the structure of candidate
molecules, a CPU intensive step. The all-atoms-pairs-shortest-path similarity
test chosen [Carhart, et al. 1985] is a robust graph-only fitness function.
The fitness function algorithm was as follows:
-
Each atom is given an extended type consisting of a tuple containing the
atomic-element and the number of single, double, and triple bonds the atom
participates in. For example, the carbon in carbon dioxide is represented
by the tuple (C,0,2,0). The C indicates that the atom is carbon. The zeros
indicate that the atom participates in no single or triple bonds. The 2
indicates that the atom participates in two double bonds.
-
The shortest path between each pair of atoms is found.
-
A bag is constructed with one set-element for each atom pair. A bag is
a set that may contain duplicate set-elements. Each set-element in the
bag is a tuple consisting of the sorted extended types of the two
atoms and the length of the shortest path between them. For example, the
set-element representing the carbon and one oxygen in carbon dioxide would
be represented by: ((C,0,2,0),(O,0,1,0),1). The first two parts of the
tuple are the extended types (also tuples) of the atoms. The 1 is the length
of the path between them.
-
The fitness of each candidate molecule is the distance between its bag
and the similarly constructed bag of a target molecule. The distance measure
used is the Tanimoto index. This is:
|c intersection t| / |c union t|
where c is the candidate's bag and t is the target's bag. Two
elements are considered identical for the purpose of the intersection and
union operators if the atoms have the same extended types and the distance
between them is the same. Each duplicate in the bag is considered a separate
set-element for the purpose of the intersection and union operators. The
Tanimoto index always returns a number between 0 and 1. We prefer fitness
functions that return lower numbers for fitter individuals, so we subtract
the Tanimoto index from one to get the fitness.
The fitness function can not only find similar molecules, which is useful
in drug design, but can also lead evolution to the exact molecule used
as the target. This can prove that the algorithm can find particular molecules.
In addition, the number of generations to find the target provides a crude
quantitative measure of performance.
Digital Logic
For digital logic circuit evolution, we attempted to evolve correct 15-step
delay, parity, and one-bit add serial circuits. By "serial circuit" we
mean that only one bit is input and output at each time step. The fitness
of a circuit was the percentage of wrong output bits generated when processing
100 random input bits. Thus, a score of zero indicated a perfect circuit
and a score of one a totally incorrect circuit. The circuits were simulated
by assuming that every device (vertex) and wire (edge) required unit processing
time . While this is not particularly realistic, it is easy and quick to
implement and is sufficient to exercise the directed graph crossover operator.
No attempt was made to generate optimal circuits, a task of greater interest
to the digital hardware community.
Some initial runs ran out of memory when the circuits became extremely
large. To reward parsimony, a fitness penalty of one percent was assessed
against a circuit for each additional edge or vertex the circuit grew above
a certain size. The penalty-free size was chosen to be well above that
necessary to create the circuit.
Experimental Setup
All computational experiments were run using the Condor cycle-scavaging
batch system [Litzkow, et al. 1988] managing approximately 150 SGI workstations
at
NASA's NAS supercomputer center [Globus, et al. 2000]. Condor watches
a "pool" of desktop workstations. When a workstation appears to be unused,
Condor
will match a waiting job with the workstation. Jobs are removed from
workstations when a keystroke or mouse motion is detected. Each genetic
algorithm run was a single Condor job.
Molecules
To see if JavaGenes could find molecules of interest, we tried to find
the following targets:
-
 benzene
(C6H6) a simple ring molecule.
benzene
(C6H6) a simple ring molecule.
-
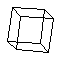 cubane (C8H8)
a cage molecule.
cubane (C8H8)
a cage molecule.
-
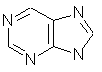 purine (C5H4N4)
fused rings and heteroatoms.
purine (C5H4N4)
fused rings and heteroatoms.
-
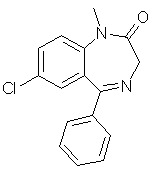 diazepam (C16H13ClN2O)
used in [Carhart, et al. 1985].
diazepam (C16H13ClN2O)
used in [Carhart, et al. 1985].
-
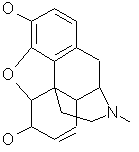 morphine (C17H19NO3)
Dr. Wipke's group has worked on morphine analog design for many years.
morphine (C17H19NO3)
Dr. Wipke's group has worked on morphine analog design for many years.
-
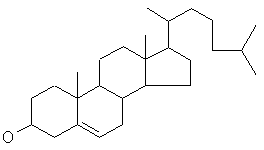 cholesterol
(C27H46O) a non-drug molecule.
cholesterol
(C27H46O) a non-drug molecule.
Stereochemistry and hydrogens are left out of the molecular diagrams
since JavaGenes does not believe in them.
Digital Logic
We attempted to evolve thee different serial circuits:
-
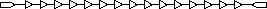 15-unit delay
15-unit delay
-
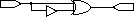 parity
parity
-
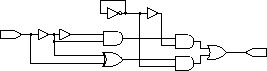 1-bit add. Note that this circuit
wouldn't work in hardware, but because our simulator assumes unit propagation
delays for every device and wire, the simulated circuit will perform
properly.
1-bit add. Note that this circuit
wouldn't work in hardware, but because our simulator assumes unit propagation
delays for every device and wire, the simulated circuit will perform
properly.
Results
31 runs (each run is one execution of JavaGenes) with identical input parameters
(except the random number seed) were conducted for each experiment. The
number of generations and population sizes were varied. Once the target
was found, runs stopped. Runs also stopped after a fixed, maximum number
of generations. We use the number of generations to find a perfect individual
as a performance measure. Combined with the population size, this provides
a quantitative measure of performance, although the precise values should
not be taken too seriously. Even with 31 runs per experiment, variation
between experiments with identical input parameters (other than the random
number seed) was observed (see the comparison
of purine and diazepam runs below). We display the results as
line graphs where the horizontal axis is generations and the vertical axis
is the percent of runs that had found a perfect individual. Thus, all curves
will be monotonically increasing. Rapidly rising curves indicate that the
target was found quickly. Curves that do not reach 100% indicate
that not all runs found the target.
Finding Small Molecules
First we examine JavaGenes performance searching for three small molecules
using a population size of 25 and a maximum of 1,000 generations:
Finding Benzene, Cubane, and Purine
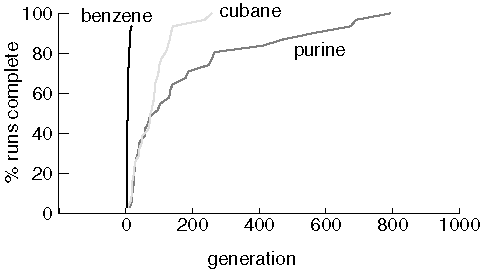
Note that two benzene jobs did not find the target at all, even though
benzene was usually found in just a few generations. The runs that could
not find benzene lost all of the cycles in the population in the first
generation created by crossover. When a population consists entirely
of non-cyclic molecules, the crossover operator can not generate cycles.
Finding Larger Molecules
Now we examine JavaGenes performance searching for three larger molecules
using a population of 500 and a maximum of 5,000 generations.
Finding Diazepam, Morphine, and Cholesterol
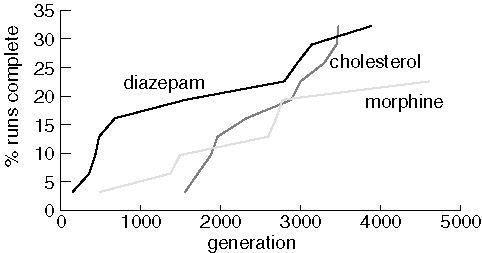
Although each run consisted of 31 jobs, only ten runs found diazepam
and cholesterol, and only seven runs found morphine. Note that JavaGenes
performance is much poorer on these larger molecules. Presumably, this
is because the size of the space-of-all-molecules explodes combinatorially
as molecule size increases. We also noticed that some populations lost
all of the rare elements in the target. For example, diazepam has only
one chlorine and one oxygen atom. Several of the diazepam jobs lost all
of one these elements from the population and were forever doomed. Interestingly,
runs that lost all oxygen and/or chlorine from the population did so within
about 400 generations. Using vertex mutation should avoid this situation,
but this paper is concerned with the properties of the crossover operator.
Now we examine JavaGenes performance searching for the same three molecules
using a population of 1,000 and a maximum of 10,000 generations.
Finding Larger Molecules with a Larger Population
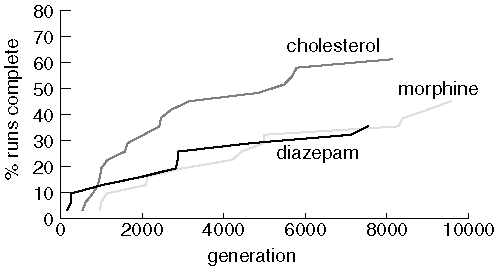
Performance is improved with a larger population and more generations,
but 20 runs still failed to find diazepam, 17 couldn't find morphine, and
12 failed to find cholesterol.
Effects of Population Size
We now examine the effects of population size by showing the results of
searching for purine with a population size of 25, 50, and 100:
Finding Purine With Different Population Sizes
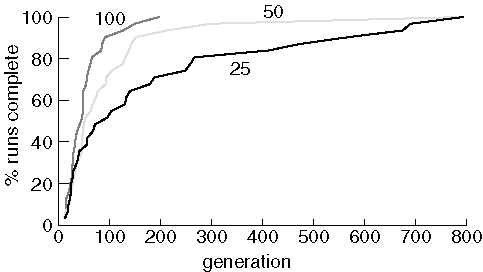
As expected, increasing the population size improves performace.
Variability Between Runs
To investigate variability, we ran five experiments of 31 runs each looking
for purine using identical parameters (except random number seeds).
Population size was 100.
Identical Experiments Finding Purine
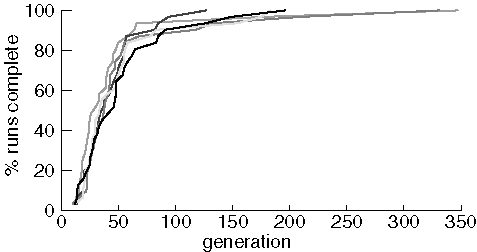
The variability between experiments is quite small for this molcular
target. Most of the difference appears in the last two or three runs
to find purine from each experiment. To see if variablity was different
with a more difficult target, we compare two experiments searching for
diazepam using a population size of 500 and a maximum of 5,000 generations:
Identical Experiments Finding Diazepam

Note that although each run consisted of 31 jobs, only 7 and 10 runs,
respectively, were able to find diazepam in 5,000 generations. Nonetheless,
although one experiment clearly out-performed the other, the results of
the two experiments are roughly comparable.
Finding Circuits
JavaGenes was able to successfully find the small circuits that implement
delay and parity functions. We compare results finding parity using a population
of 600 and finding delay with populations of 200 and 600. In all
cases, the maximum number of generations was 5,000:
Finding Circuits
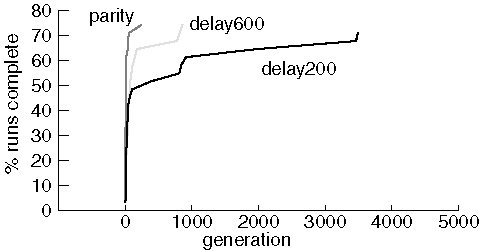
Note that only 22-24 (out of 31) runs succeeded in finding a proper
circuit in each experiment. Results are very similar for most of the successful
runs with substantial variability only for the worst performing runs that
succeeded. In spite of many attempts, we were never able to evolve a perfect
1-bit add circuit. The source of the problem is unclear, although it may
be that the crossover operator does not preserve useful sub-graphs very
often.
Progress of a Run
This figure shows the fitness of the best individual for each of 31 runs
searching for morphine. Population size was 500 and the maximum number
of generations allowed was 5,000. Each data point was 10 generations apart.
In other words, fitness data were collected from the population every 10
generations.
31 Runs Searching for Morphine
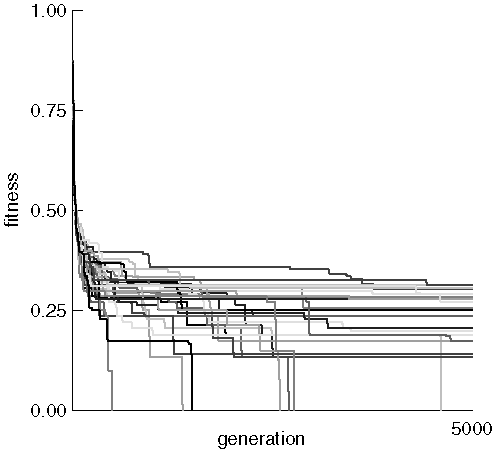
The initial random populations all had a best individual fitness near
0.9 which quickly inproved to around 0.25. Most runs then leveled
off with long periods of no improvement, occasionally punctuated by sudden
bursts of increasing fitness. Notice that morphine was often found
even when the previous best fitness was quite poor, as evidenced by the
long verticle lines ending at the x-axis. This indicates that fitness
improved very rapidly over the course of a few tens of generations.
We now examine the mean fitness of each run in the same experiment:
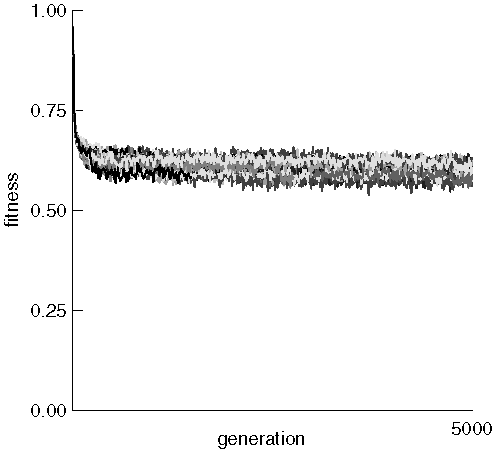
The mean fitness of each run dropped rapidly from about 0.96 to somewhere
near 0.6 and stayed there with only very minor improvement. This may be
caused by the extremely destructive nature of the crossover operator, which
can be expected to generate many very unfit children from fit parents.
Eery generated child was placed back into the fixed-size population, and
there was no guarantee that the individual replaced had lower fitness than
the child. It might be interesting to develop a procedure that rarely replaces
individuals if the child has worse fitness. One might expect the average
fitness to continue to improve as evolution proceeds.
Effect of the "Coin Flip" Step
As mentioned before, [Globus, et al. 1999] provided results from the crossover
algorithm, but with a bug that effectively eliminated the "flip coin" step
in fragment combination. The results discussed above used code with additional
modifications beyond the bug fix, primarily in the way that the initial
population was generated. Table 1 compares performance before and
after the bug fix, with no other code modifications. Input parameters were
identical except for the number of runs per experiment and the random number
seeds for each run. The numbers in parentheses refer to results from
[Globus, et. al 1999].
Table 1: Finding Small Molecules With and (Without) "Coin Flip"
Step
31 runs for
each molecule
(20 with bug) |
Population size |
Median generations to find target |
Minimum generations to find target |
Number of runs that failed to find target |
Maximum generations
|
| Benzene |
100 (200)
|
3 (39.5)
|
0 (2)
|
0 (8)
|
10 (1000)
|
| Cubane |
100
|
20 (46.5)
|
4 (13)
|
0 (0)
|
140(NR)
|
| Purine |
100
|
38 (245)
|
6 (19)
|
0 (4)
|
269(1000)
|
NR = not recorded. Because of run-to-run variability, and because many
runs did not complete, median, rather than mean, generations to find the
target is used, a procedure suggested by [Claerbout and Muir 1973].
Diazepam, morphine, and cholesterol were never found more than once
each in [Globus, et al. 1999]. The difference in results before and after
the bug fix show the importance of the "coin flip" step.
Comparison with Random Search
To see if our crossover operator was better than random search, we searched
for purine under three conditions: crossover alone, generating random molecules
using the same algorithm as for the initial population (random search),
and a 50-50 mix of crossover and random search. Twenty-one runs of
1000 generations on a population of 200 were conducted in each case. The
[Globus, et al. 1999] algorithm was used. The fixed algorithm should do
even better.
Comparison With Random Search
| case |
percent of runs that found purine |
median generations to find purine |
| random search |
0
|
N/A
|
| crossover alone |
100
|
37
|
| 50-50 mix of crossover and random search |
100
|
48
|
Clearly the crossover operator is better than random search.
Summary
Using our crossover operator, and the more obvious mutation operators,
genetic algorithms may now be applied to graph representations. Our results
show that genetic algorithms with a graph representation can evolve a variety
of molecules and very simple circuits. Significant additional work will
be required to determine if applying genetic algorithms using a graph representation
to molecular design is beneficial, but our results are encouraging. Unfortunately,
we were not able to evolve non-trivial circuits. Even the simple delay
and parity circuits were difficult to evolve. This may be due to dividing
circuits into fragments with a single input or output vertex each.
This division may not preserve useful sub-units very often. An alternate
crossover operator that choses a subgraph that does not include either
the input or output vertex as one fragment might perform better.
The space-of-all-graphs is not well understood or characterized.
Therefore, it is reasonable to presume that searching for graphs using
genetic algorithms may be profitable in a number of domains. Our
crossover operator is quite general, functions on both directed and undirected
graphs, is unbiased, and can operate on all forms of cyclic and non-cyclic
graphs. Using crossover alone, with no mutation, moderate sized pharmaceutical
drug molecules can often be evolved within a few thousand generations with
a population of only 1,000.
Acknowledgments
Many thanks to Daniel Tunkelang, formerly of Carnegie Mellon, for providing
his Jiggle code [Tunkelang 1998]. Jiggle arranges arbitrary graphs for
easy viewing. Thanks to NWP Associates, Inc. for providing their Student
T-Test code. Thanks to Rich McClellan, University of California at Santa
Cruz, for providing the mol file reading and atomic element code. Thanks
to Gail Felchle for much of the graphics art work. Thanks to Bonnie Klein,
Jason Lohn, and Deepak Srivastava for reviewing this paper. This work was
funded by NASA Ames contract NAS 2-14303.
References
[Baeck, et al. 1997] Thomas Baeck, Ulrich Hammel, and Hans-Paul Schwefel,
"Evolutionary Computation: Comments on the History and Current State,"
IEEE
Transactions on Evolutionary Computation, volume 1, number 1, pages
3-17, April 1997.
[Carhart, et al. 1985] Raymond Carhart, Dennis H. Smith, and R. Venkataraghavan,
"Atom Pairs as Molecular Features in Structure-Activity Studies: Definition
and Application," Journal of Chemical Information and Computer Science,
volume 23, pages 64-73.
[Claerbout and Muir 1973] J. F. Claerbout and F. Muir, ``Robust Modeling
with Erratic Data,'' Geophysics, volume 38, pages 826-844.
[Corey and Wipke 1969] E. J. Corey and W. Todd Wipke, "Computer-Assisted
Design of Complex Organic Syntheses," Science, volume 166, pages
178-192, 10 October 1969.
[De Jong 1990] K. A. De Jong "Introduction to the Second
Special Issue on Genetic Algorithms," Machine Learning, 5 (4), 1990.
[Globus, et al. 1999] Al Globus, John Lawton, and Todd Wipke, "Automatic
Molecular Design Using Evolutionary Techniques," Nanotechnology,
volume 10, number 3, September 1999, pages 290-299.
[Globus, et al 2000] Al Globus, Eric Langhirt, Miron Livny, Ravishankar
Ramamurthy, Marvin Solomon, Steve Traugott, "JavaGenes and Condor: Cycle-Scavenging
Genetic Algorithms," Java Grande 2000, sponsored by ACM SIGPLAN, San Francisco,
California, 3-4 June 2000.
[Holland 1975] John H. Holland, Adaptation in Natural and Artificial
Systems, University of Michigan Press.
[Koza 1992] John R. Koza, Genetic Programming: on the Programming
of Computers by Means of Natural Selection, MIT Press, Massachusetts,
1992.
[Koza, et al. 1997] John R. Koza, Forrest H. Bennett III, David Andre,
Martin A. Keane and Frank Dunlap, "Automated Synthesis of Analog Electrical
Circuits by Means of Genetic Programming," IEEE Transactions on Evolutionary
Computation, volume 1, number 2, pages 109-128, July 1997.
[Koza, et al. 1999] John R. Koza, Forrest H. Bennett, Martin A. Keane,
Genetic
Programming III : Darwinian Invention and Problem Solving, Morgan Kaufmann
Publishers, ISBN: 1558605436.
[Litzkow, et al. 1988] M. Litzkow, M. Livny, and M. W. Mutka, "Condor
- a Hunter of Idle Workstations,'' Proceedings of the 8th International
Conference of Distributed Computing Systems, pp. 104-111, June1988.
See http://www.cs.wisc.edu/condor/.
[Lohn and Colombano 1998] Jason D. Lohn and Silvano P. Colombano, "Automated
Analog Circuit Synthesis Using a Linear Representation,'' Second International
Conference on Evolvable Systems: From Biology to Hardware, Springer-Verlag,
23-25 September 1998.
[Nachbar 1998] Robert B. Nachbar, "Molecular evolution: a Hierarchical
Representation for Chemical Topology and its Automated Manipulation," Proceedings
of the Third Annual Genetic Programming Conference, University of Wisconsin,
Madison, Wisconsin, 22-25 July 1998, pages 246-253.
[Quarles, et al. 1994] T. Quarles, A. R. Newton, D. O. Pederson, and
A. Sangiovanni-Vincentelli,
SPICE 3 Version 3F5 User's Manual, Department
of Electrical Engineering and Computer Science, University of California
at Berkeley, CA, March 1994.
[Teller 1998] Astro Teller, "Algorithm Evolution with Internal Reinforcement
for Signal Understanding," Computer Science PhD Thesis, Carnegie Mellon
University, Publication Number: CMU-CS-98-132.
[Tunkelang 1998] Daniel Tunkelang, A
Numerical Optimization Approach to Graph Drawing, Dissertation, Carnegie
Mellon University, School of Computer Science, December 1998.
[Weininger 1995] David Weininger, "Method and Apparatus for Designing
Molecules with Desired Properties by Evolving Successive Populations,"
U.S. patent US5434796, Daylight Chemical Information Systems, Inc.




 benzene
(C6H6) a simple ring molecule.
benzene
(C6H6) a simple ring molecule. cubane (C8H8)
a cage molecule.
cubane (C8H8)
a cage molecule. purine (C5H4N4)
fused rings and heteroatoms.
purine (C5H4N4)
fused rings and heteroatoms. diazepam (C16H13ClN2O)
used in [Carhart, et al. 1985].
diazepam (C16H13ClN2O)
used in [Carhart, et al. 1985]. morphine (C17H19NO3)
Dr. Wipke's group has worked on morphine analog design for many years.
morphine (C17H19NO3)
Dr. Wipke's group has worked on morphine analog design for many years. cholesterol
(C27H46O) a non-drug molecule.
cholesterol
(C27H46O) a non-drug molecule. 1-bit add. Note that this circuit
wouldn't work in hardware, but because our simulator assumes unit propagation
delays for every device and wire, the simulated circuit will perform
properly.
1-bit add. Note that this circuit
wouldn't work in hardware, but because our simulator assumes unit propagation
delays for every device and wire, the simulated circuit will perform
properly.







