Enabling
Computational Nanotechnology through JavaGenes in a Cycle Scavenging
Environment
Al Globus,a Madhu Menon,b and Deepak Srivastavaa
(a) NASA Ames Research Center, CSC/NAS, Moffett Field, CA 94035
(b) Center for Computational Sciences and Department of Physics, University of Kentucky, Lexington, KY 40506-0045
Abstract: A genetic algorithm procedure is
developed and implemented for fitting parameters for many-body inter-atomic
force field functions for simulating nanotechnology atomistic applications
using portable Java on cycle-scavenged heterogeneous workstations. Given a
physics based analytic functional form for the force field, correlated
parameters in a multi-dimensional environment are typically chosen to fit
properties given either by experiments and/or by higher accuracy quantum
mechanical simulations. The implementation automates this tedious procedure
using an evolutionary computing algorithm operating on hundreds of
cycle-scavenged computers. As a proof of concept, we demonstrate the procedure
for evaluating the Stillinger-Weber (S-W) potential by (a) reproducing the
published parameters for Si using S-W energies in the fitness function, and (b) evolving a “new” set of parameters using
semi-empirical tight-binding energies in the fitness function. The “new”
parameters are significantly better suited for Si cluster energies and forces
as compared to even the published S-W potential.
1. Introduction: Accurate molecular dynamics (MD)
simulation of reactive systems containing many atomic species is important for
the conceptualization, design and testing of novel nanoscale materials,
molecular electronic devices, nano-integrated systems and applications, and a
broad range of physical and chemical phenomenon in other areas as well. The
physical and chemical characterization of carbon nanotubes and fullerenes,
design and operations of molecular gears, hinges, three-way junctions, and
bearings have also utilized MD simulations using reactive dynamics of 2- or
3-atomic species containing systems [Globus et al. 1998, Srivastava et. al.
2001]. However, as the system and device sizes continue to shrink and
composition becomes more multi-species, there is an urgent need for developing
good quality reactive atomic force field functions that are not currently available.
There are two parts to developing atomic force field functions. First, finding an analytic functional form that reflects the physical and chemical nature of the atomic species under consideration, and second, fitting parameters in a complex multi-dimensional parameter space based on the data available from the experiments or more accurate quantum mechanical calculations. In an ideal case, the cycle of choosing a functional form and parameterization of the force field function should be iterated until a reasonable convergence on the choice of inter-atomic potentials is achieved. Doing this for multi-component systems is extremely tedious because the parameter space that needs to be investigated is large and may be coupled in a complex way. The tedium has deterred regular successful attempts in developing “new” force field functions and improving upon the existing ones for a variety of nanotechnology applications.
Using a Genetic Algorithm (GA) in the proposed scheme has two advantages. First, GA is geared towards sampling both the near-equilibrium (minimum energy) and far-from-equilibrium (energetically excited) configurations in the data-set, and second, thousands of independent GA jobs can be run in an embarrassingly parallel manner on cycle-scavenged non-homogeneous distributed computing resources. JavaGenes is a general purpose GA code written in Java [Globus, et al. 2000] to evolve molecules and modified for this work. The executables run on nearly any modern computer without modification. In this work, we demonstrate the power of JavaGenes and cycle-scavenging by automating the development of new fitting parameters for the well established Stillinger-Weber (S-W) Si potential. Indeed, literally dozens of high quality parameterizations are found by thousands of JavaGenes jobs executed by cycle scavenging approximately 350 workstations at NASA’s NAS supercomputing facility.
GA has been used to find atomic interaction potential parameters for “non-reactive” force fields for metal-organic systems [Mohamadi, et al. 1990], tripod metal compounds [Hunger, et al. 1998, Hunger, et al. 1996, Hunger and Huttner 1999] and Technetium (Tc) complexes [Cundari and Fu 2000]. Wang and Kollman have optimized Amber force field parameters for several organic molecules using GA [Wang and Kollman 2001]. Since these force fields do not allow reactions, they are unsuited to many nanotechnology applications.
2. Method: In this section we briefly describe the implementation of JavaGenes for massively parallel search of the multi-parameter space for fitting reactive many-body atomic force field functions.
2a. JavaGenes
Implementation: GAs
seek to mimic natural evolution's ability to produce highly functional objects.
Natural evolution produces organisms, whereas GAs can produce sets of
parameters, programs, molecular designs, and many other structures. Our
GA, JavaGenes, employs the following algorithm (words in quotes are typical GA
terminology):
- Represent potential parameters with a
set of floating point numbers; each set is called an
"individual"
- Generate a "population" of
individuals with random parameters
- Calculate the "fitness" of
each individual
- Repeat
- Randomly select
"parents" with a bias towards better fitness
- Produce
"children" from the parents with either a:
- "crossover"
that combines parts of two parents into a child
- or
"mutation" that modifies a single parent
- Calculate the fitness
of the child
- Randomly replace
individuals of less fitness in the population with the thus produced
children
- Until satisfied according to some minimal
convergence criteria
The vast majority of the CPU time is spent calculating the fitness function and each fitness function evaluation is entirely independent of the others. This means that a single GA run is almost embarrassingly parallel, but we do not take advantage of this because many runs are necessary to evaluate a stochastic procedure. Rather, each of 1000s of runs is submitted to the Condor batch queue. Since there are only 350 machines in our Condor pool, this is perfectly adequate parallelization.
JavaGenes is a steady state tournament selection genetic algorithm. The tournament size is usually two. In tournament selection each parent is chosen by randomly selecting two individuals from the population and choosing the fittest to be the parent. After crossover or mutation produces a child, individuals to replace are chosen by an anti-tournament of size two. An anti-tournament chooses the least fit individual.
We represent force field parameters as a ragged two-dimensional array of double precision floating point numbers. The first dimension represents the two- or three-body terms of the potential function, and the ragged second dimension holds the varying number of parameters depending on the number of bodies. Each parameter is assigned a set of limits within which it is allowed to evolve. The limiting values of the parameters are chosen from the physical interpretation of the contribution of the parameter to the force field function and are randomized among jobs.
Evolution is guided by a fitness function. The fitness function must provide a fitness for any possible individual, no matter how bad, and distinguish between any two individuals, no matter how close they are. The fitness function for this work compares energies and forces computed for a given set of atomic conformations using the evolving parameters with externally supplied energies and forces. Conformations for both near equilibrium and far from equilibrium configurations for very high and low energies were used.
In general GA is not guaranteed
to find a unique or even a satisfactory solution, but often works well in
practice. JavaGenes uses many “GA parameters” (mutation rate, tournament size,
etc.) that can affect performance and results of the search procedure. Choosing
GA parameters is a non-trivial problem. We solve this by randomizing the choice
of GA parameters in appropriate ranges in many parallel GA jobs. This
eliminates a tedious human-directed search for good GA-parameters. Initially,
30-100 single-workstation GA runs with identical GA-parameters (except the
random number seed) for each job
were run with populations varying between 1000-3000. The GA-parameters that
worked for one search (say, Si dimers in the fitness function) would fail in a
similar search for a different system (say, larger Si clusters). The alternate
technique of using a thousand trajectories with randomized GA-parameters and
smaller populations (100-200) worked very well for all the systems attempted.
2b. Example: Stillinger-Weber (S-W)
Many-body Potential
We have chosen the S-W functional form as an example and fitted the parameters using the GA approach in two cases: energies and forces calculated by S-W with the original parameters, and energies and forces calculated by a semi-empirical tight-binding code [Menon and Subbaswamy 1993]. The S-W molecular potential expresses the total energy of a given configuration in terms of the sum of two- and three-body contributions to the energy as a function of the atomic positions in the configuration:
![]()
![]()
where E is total interaction energy, i,j,k indicate individual atoms, and v is the interaction energy of n atoms. To reduce computation, reactive potentials often have a cutoff function which forces each term to zero at large atomic separations. This converts the problem from O(n3) to O(n) since only near neighbors need be considered and the number of near-neighbors is limited by the minimum bond length found in systems at reasonable temperatures and pressures (outside of neutron stars, black holes, etc.).
The v terms are:
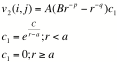
where r is the i,j inter-atomic distance and all other values are adjustable parameters; and
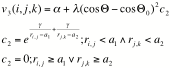
where rij and rjk are the two inter-atomic distances, theta is the angle and all other values are adjustable parameters.
2c. CPU Cycle Scavenging System: Condor
We use the Condor [Litzkow, et al. 1988] cycle scavenger running on about 350 SGI and Sun machines at the NASA Advanced Supercomputing (NAS) Division. Each machine runs a daemon that watches user I/O and CPU load. Multi-processor machines run one daemon for each processor. When a CPU has been idle for 2 hours, a job from the batch queue is assigned to the CPU and will run until the daemon detects a keystroke, mouse motion, or high non-Condor CPU usage. At this point, the job is removed from the workstation and placed back on the batch queue. The job eventually runs again, although probably on a different machine. Typically, between 100-200 NAS machines are available for batch processing through the NAS Condor pool at any particular time. Figure 1 shows a typical month’s usage on NAS condor pool. Note the usage spikes during the weekday.
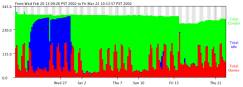
Figure 1: The horizontal axis is time, the vertical axis number of processors. Red indicates processors in normal use, blue idle, and green indicates the processors running Condor jobs.
While cycle-scavenging systems can supply huge amounts of CPU, they are restricted to embarrassingly parallel problems with minimal I/O requirements. Many important problems fit within these restrictions, including parameter studies, Monte Carlo simulations, data analysis and GA.
We discovered that, when running thousands of jobs, a few would die before completion for various reasons. Occasionally the Java Virtual Machine (JVM) would crash, jobs would receive kill signals from unknown causes, and so forth. Fortunately, losing a few percent of the jobs doesn’t matter since we are only interested in the best dozen or so parameter sets. More seriously, black holes (machines that kill all jobs assigned to them) develop occasionally. Black holes at NAS are usually caused by an incorrect Java installation or a full disk. We added a check for a missing JVM in the TCL script that runs each JavaGenes job. Jobs report the error and wait for the installation to be corrected. Full disks are discovered by large numbers of dead-job emails (Condor sends email when a job completes). In this case, the black hole is fixed or removed from the pool and the jobs are restarted.
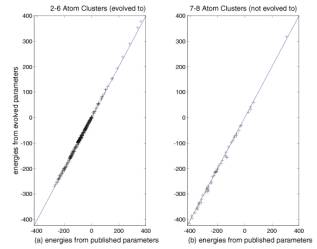
3. Results: First, as validation, we use the
published S-W potential parameters to calculate energies and forces of small Sin
(n = 2 - 6) clusters for the fitness function, and compare the results in the
case of Sin (n =7, 8) clusters that were not used in the fitness
function. Figure 2 compares the energies of Si clusters as calculated by S-W
potential with GA evolved parameters with those computed by using the published
parameters in two cases. Figure 2 (a)
is for Sin clusters with n = 2 - 6, Figure 2 (b) is for Sin
clusters with n = 7, 8, i.e., the clusters not used in the fitting procedure.
The figure shows the comparison of the energies in the full range of the
configurations. The comparison shows a good fit in both cases.
Figure 2: Comparison of energies (in kcal/mol) calculated for Si2-8 clusters using the evolved (with S-W fitness function) and published parameters. Each cross represents a cluster. Crosses on the diagonal line are a perfect fit between the evolved and published values: (a) for Si2-6 used in the fitness function., and (b) for Si7,8 not used in the fitness function.
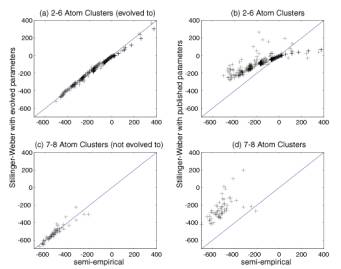
Second, as a test of the approach, we find “new” GA evolved
S-W potential parameters where the fitness function was described by energies
and forces of small Si clusters computed from a non-orthogonal quantum
tight-binding scheme (labeled semi-empirical in the figures). The results are
shown in Figure 3 (a) and (c). The match is very good for 2-6 atom Si clusters,
as might be expected, because the energies and forces for these clusters were
used in constructing the fitness function. The comparison of the energies of 7,
8 and 33 atom Si clusters, which were not used in the fitting procedure, also
show good results suggesting that the approach is transferable. Figure 3 (b)
and (d) shows the comparison of energies calculated with evolved (with
tight-binding fitness function) parameters with those calculated from the
published parameters. Figure 4 shows similar results for Si33
clusters. In both cases the evolved parameters have a much better fit to the
tight-binding energies. This means that using GA we have significantly improved
upon the original parameterization of S-W by a “new” set that describes Si
cluster energetics rather well.
Figure 3: Comparison of energies (kcal/mol) calculated for clusters using the evolved (a,c) and published S-W parameters (b,d). Figures (a) and (b) are for Si2-6 (used in the fitness function), and (c) and (d) are for Si7,8 (not used in the fitness function).
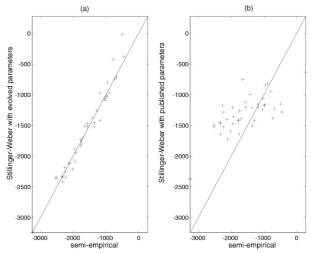
Figure 4: Same as Figure 3, but for Si33 clusters that were not used in the fitness function. (a) compares with the evolved parameters, (b) with the original published parameters.
4. Computational Issues: Figure 5 shows job length distribution for 96 jobs typical of the jobs in this study. The time variation reflects execution on different machines and different checkpoint histories. In particular, the handful of jobs with very long times reflect slow machines in the Condor pool that are almost never used. Such machines may run a single job for days without being killed because no one ever logged in. JavaGenes checkpoints jobs (using Java serialization) every hour. If a job is killed between checkpoints, then the results since the last checkpoint are lost and evolution will restart from the checkpoint with a different random number seed.
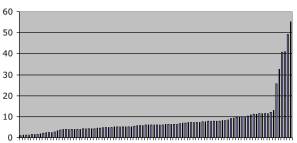
Figure 5: The horizontal axis is individual jobs sorted by total execution time. The vertical axis is time in hours. The execution time includes the time between a checkpoint and removal from a machine, i.e., time that does not contribute to the final result. Mean = 8.3 hours, median = 6.3 hours, min = 0.9 hours, and max = 55.3 hours.
5. Impact: Given a functional form, for
molecular force field functions, we have shown that genetic algorithms (GA)
show promise for automating the task of fitting parameters over a complex range
of configurations using large amounts of otherwise unused compute cycles in a
distributed non-homogeneous computing environment. However, very substantial
CPU resources are needed in part because we randomize the GA parameters and
therefore need hundreds to thousands of GA jobs to get good results. This is
not a problem, because the jobs are embarrassingly parallel with low IO
requirements and are suited for cycle-scavenging computation. This work
suggests that these otherwise wasted resources can be used to enable next generation simulation tools for complex
many-atomic species systems in nanotechnology designs and applications of the
future.
6. Acknowledgments: We thank NASA's NAS supercomputing facility for funding and computational support through the CICT program ITSR project. Part of this work (AG and DS) is supported by NASA contract 704-40-32 to CSC.
7. References
[Cundari and Fu 2000] T. R. Cundari, W. T. Fu, "Genetic Algorithm Optimization of a Molecular Mechanics Force Field for Technetium," Inorganica Chimica Acta, 300-302, pages 113-124, 2000.
[Globus et al. 1998] "Machine Phase Fullerene Nanotechnology," Al Globus, Charles Bauschlicher, Jie Han, Richard Jaffe, Creon Levit, Deepak Srivastava, Nanotechnology, 9, number 2, September 1998, pages 192-199.
[Globus et al. 2000] "JavaGenes and Condor: Cycle-Scavenging Genetic Algorithms," Al Globus, Eric Langhirt, Miron Livny, Ravishankar Ramamurthy, Marvin Solomon, and Steve Traugott, Java Grande 2000, sponsored by ACM SIGPLAN, San Francisco, California, 3-4 June 2000.
[Hunger, et al. 1996] J. Hunger, S. Beyreuther and G. Huttner, “Modeling of Tripod Metal Compounds RCH2C(CH2PR'R")3MLn: Optimization of Force Field Parameters by Genetic Algorithms,” Journal of Molecular Modeling 2, 257, 1996.
[Hunger, et al. 1998] J. Hunger, S. Beyreuther, G. Huttner, K. Allinger, U. Radelof and L. Zsolnai, “How to Derive Force Field Parameters by Genetic Algorithms: Modeling tripod-Mo(CO)3 Compounds as an Example,” European Journal of Inorganic Chemistry, pages 693-702, 1998.
[Hunger and Huttner 1999] J. Hunger and G. Huttner, “Optimization and Analysis of Force Field Parameters by a Combination of Genetic Algorithms and Neural Networks,” Journa l of Computational Chemistry, volume 20, pages 455-471, 1999.
[Litzkow, et al. 1988] M. Litzkow, M. Livny, and M. W. Mutka, "Condor - a Hunter of Idle Workstations,'' Proceedings of the 8th International Conference of Distributed Computing Systems, pages 104-111, June 1988. See http://www.cs.wisc.edu/condor.
[Menon and Subbaswamy 1993] Madhu Menon and K. R. Subbaswamy, "Nonorthogonal Tight-Binding Molecular-Dynamics Study of Silicon Clusters," Physical Review B, Volume 47, Number 19, pages 754-759, 15 May 1993.
[Mohamadi, et al. 1990] F. Mohamadi, N. G. J. Richards, W. C. Guida, R. Liskamp, M. Lipton, C. Caufield, G. Chang, T. Handrickson, W. C. Still, Journal of Computational Chemistry, volume 11, pages 440-467, 1990.
[Stillinger and Weber 1990] Frank H. Stillinger and Thomas A. Weber, “Dynamical Branching During Fluorination of the Dimerized Si(100) Surface: A Molecular Dynamic Study, Journal of Chemical Physics, 92(10), pages 6239-6245, 15 May 1990.
[Srivastava et al. 2001] D. Srivastava, M. Menon and K. Cho, “Computational Nanotechnology with Carbon Nanotubes and Fullerenes,” AIP & IEEE published, Computing in Engineering and Sciences, page 42, July-August 2001.
[Wang and Kollman 2001] "Automatic Parameterization of Force Field by
Systematic Search and Genetic Algorithms," Junmei Wang and Peter A.
Kollman,
Journal of Computational Chemistry, volume 22,
issue 12, pages 1219-1228.