Introduction

Fig. 1 Space-filling model of benzyne. Gray atoms are carbon and white atoms are hydrogen.
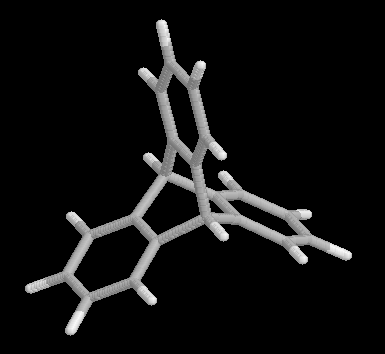
Fig. 2 Triptycene, the product of benzyne addition to anthracene.

demonstrated that the only reaction path for o-benzyne with C60 leads to the [2+2] cycloaddition product in which benzyne adds across one of the interpentagonal bonds (forming a cyclobutene ring in the process). Either reaction product results in a loss of aromaticity and distortion of the PAH or fullerene substrate, and in a loss of strain in the benzyne. It is not clear, however, why different products are preferred in these cases. Fig. 3-5 are the [2+2] and [2+4] products for addition of benzyne to naphthalene and C60, respectively. There are no experimental data available for the addition of benzyne to large fullerenes or carbon nanotubes. However, if multiple benzyne molecules could be added to nanotubes at controlled sites, the resulting products could resemble molecular paddle wheels or gears and might be useful components for nanotechnology machines (this concept is investigated in a companion paper [Han 96]).

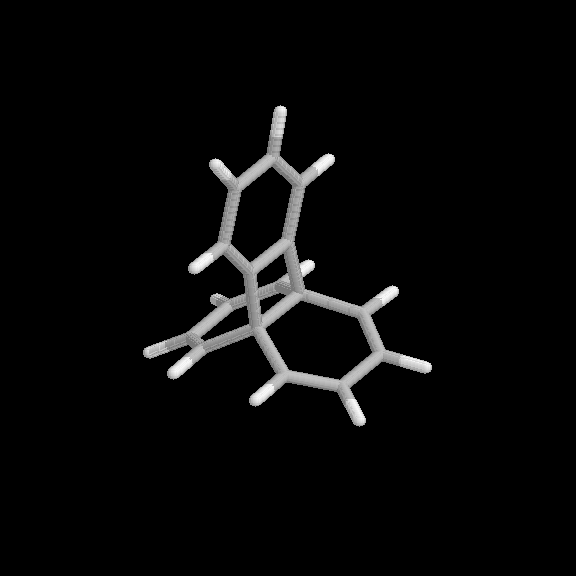
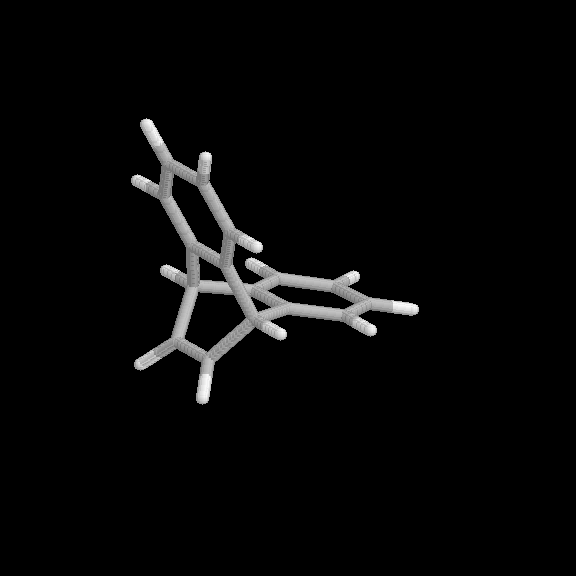
Fig. 3 Products of the benzyne-naphthalene cycloaddition reaction. (a) [2+2] product, (b) [2+4] product.

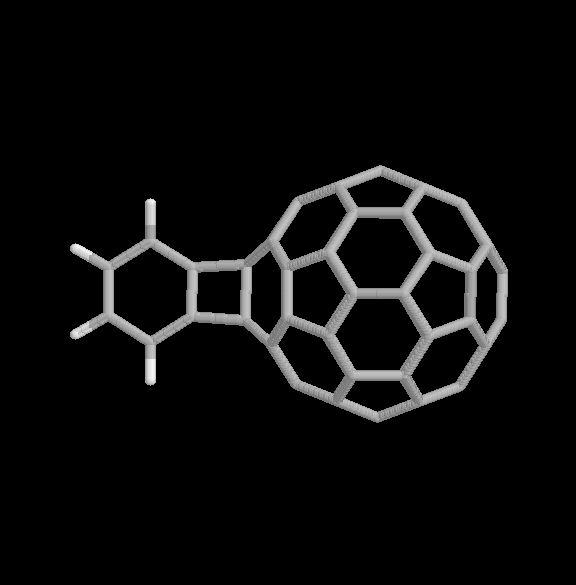
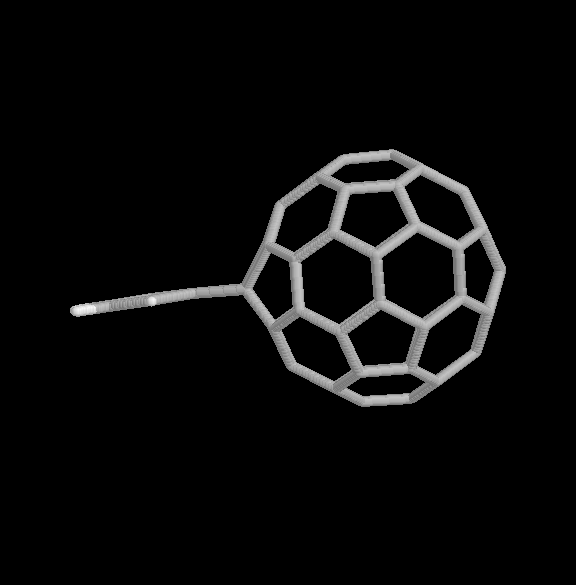
Fig. 4 [2+2] product of the benzyne-C60 cycloaddition reaction (two views).

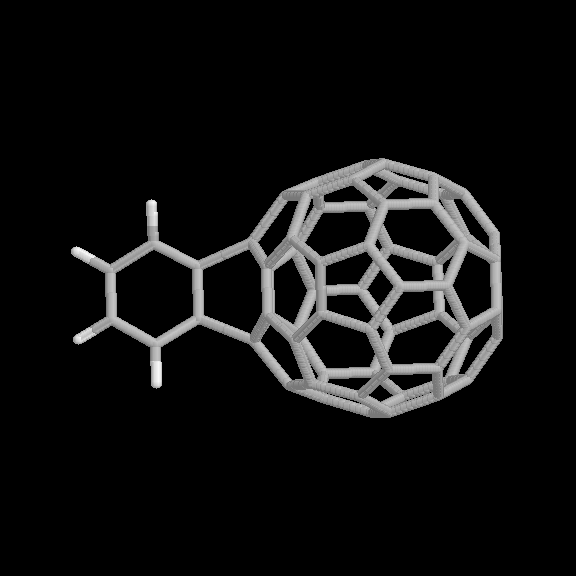
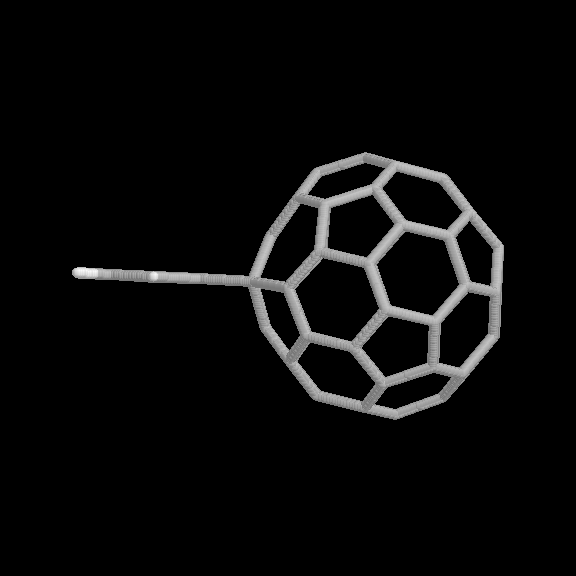
Fig. 5 [2+4] product of the benzyne-C60 cycloaddition reaction (two views).

In the current paper, we consider the stability of benzyne-nanotube adducts and the ability of Brenner's [Brenner 90] potential energy model to describe the structure and stability of these adducts. The Brenner potential has been widely used for describing diamondoid and graphitic carbon. Recently it has also been used for molecular mechanics and molecular dynamics simulations of fullerenes and nanotubes. However, it has not been tested for the case of functionalized fullerenes (especially with highly strained geometries). We use the Brenner potential for our companion nanogear simulations [Han 96] and believe that it should be calibrated to insure that those simulations are physically reasonable. In the present work, Density Functional theory (DFT) calculations are used to determine the preferred geometric structures and energetics for this calibration. The DFT method is a kind of ab initio quantum chemistry method for determining the electronic structure of molecules. For a given basis set expansion, it is comparable in accuracy to the MP2 method (better than Hartree Fock, but less accurate than more extensive electron correlation methods such as MP4 or CCSD). However, for systems with large numbers of basis functions it more efficient than any other methods that include electron correlation effects.

For the nanotube calculations, a segment of a single-walled [14,0] nanotube was generated (see [Han 96]). This tube has 14 benzene rings around the circumfrence and a diameter of 10.9 Å. The segment used in the present work is only 3 rings long, but this is adequate to describe the distortions that occur at the site where the benzyne is joined. In order to make the quantum chemistry calculations tractable, a further simplification had to be made: we used only a semicircular band to represent the nanotube, but constrained the carbon atoms at the two ends of the strip to remain 10.9 Å apart. 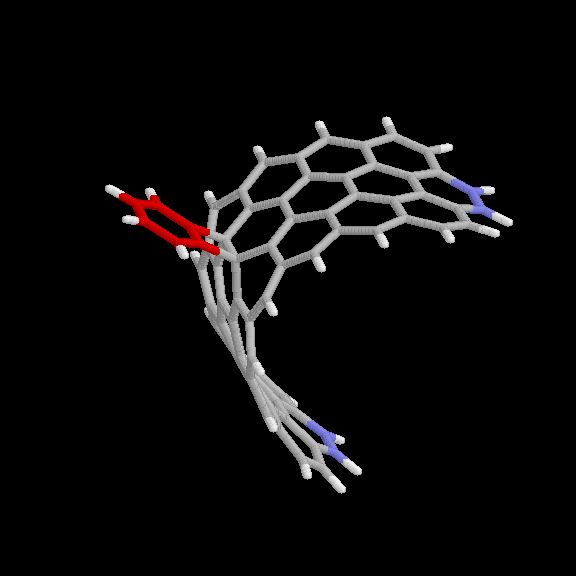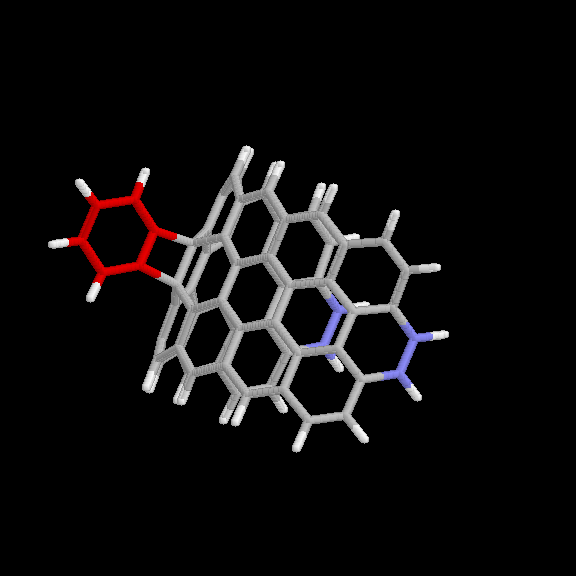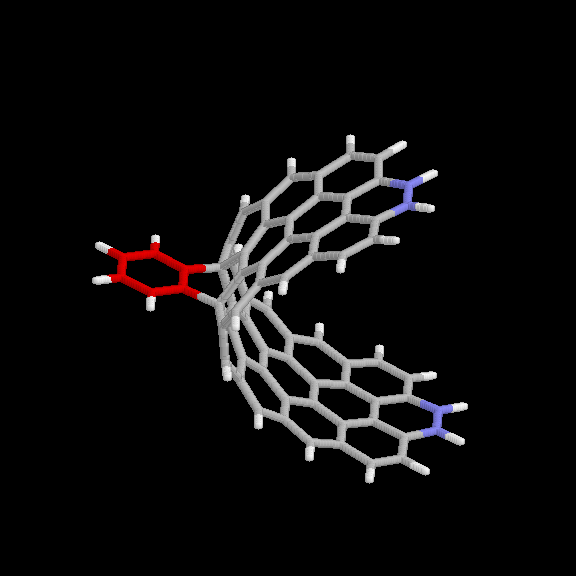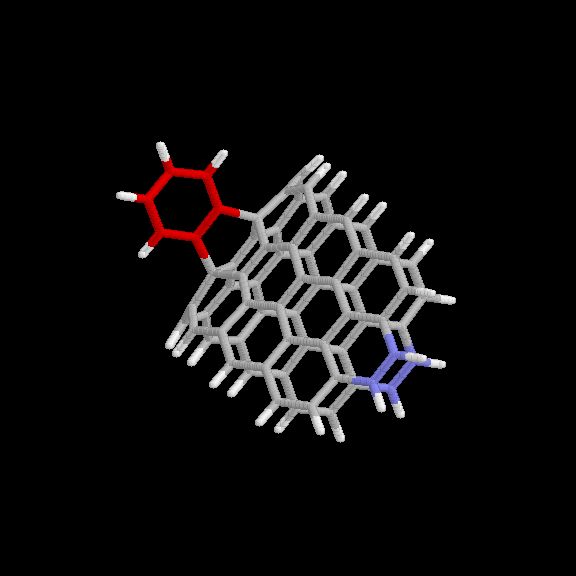This nanotube model with the benzyne adduct is given in Fig. 6 and 7. The benzyne carbon atoms are shown in red for easier visibility. The blue atoms are the end carbons subject to the distance constraint. Keeping the two ends of the strip 10.9 A apart forces it to maintain the appropriate curvature. This nanotube model (without the benzyne adduct) has the chemical formula C64H22.

Fig. 6 Model used for benzyne-nanotube reaction: [2+2] product. Red atoms are benzyne carbons; blue atoms are nanotube carbons subject to distance constraints.

Table 1. Energy of Reaction (in kcal/mol) for Benzyne Cycloaddition

Reactant	Product	STO-3G	4-31G	6-31G*	Brenner
Naphthalene	[2+4]	-67	-65	-66	-96
	[2+2]	-4	-8	-12	+5
C60	[2+4]	-25	+10		-107
	[2+2]	-108	-68		-109
Nanotube[14,0]	[2+4]	-88			-108
	[2+2]	-56			-83

For the [2+2] product, the interior naphthalene bond length increases from 1.41 to 1.60 Å and the benzyne "triple" bond increases in length from 1.22 to 1.38 Å. The bonds connecting benzyne to naphthalene are 1.53 Å long. The 4-membered ring is a planar trapezoid with angles of 95 and 85°. The dihedral angle describing the folding of the naphthalene changes by 49.4° between reactant and product (from 180 to 130.6°). Mulliken population analysis shows a modest increase of negative charge at the naphthalene connection points from -.004 to -.127 and a change in charge at the benzyne connection points from -.025 to +.063. For the [2+4] product, the connecting bonds are 1.56 Å long. The benzyne sits 1.44 Å above the original naphthalene ring plane. However the resulting adduct has 3 nearly equivalent cyclohexadiene rings and the original ring of the naphthalene is bent by 60° from planarity.

These naphthalene-benzyne adducts were subjected to various distortions to determine the stiffness of these molecules as an indicator of how well they might function as teeth in nanogears [see Han 96]. Tilting and twisting distortions refer to the position of the benzyne relative to the underlying naphthalene molecule. Tilting is the distortion largely responsible for slip in the nanogears [Han 96]. For a 10° tilt, the energy of the [2+2] product increased by 1.32 kcal/mol (5.56 kcal/mol for a 20° tilt) and the energy of the [2+4] product increased by 3.94 kcal/mol. Thus, it is seen that the [2+4] product is somewhat stiffer than the [2+2] product. A 10° twist increased the energy of the [2+2] product by 0.82 kcal/mol. We also pulled the benzyne ring away from the naphthalene. For the [2+2] product, when the benzyne is pulled off by 0.4 Å the resulting energy is 14.5 kcal higher than the asymptote, indicating the existence of an energy barrier. At this geometry, the naphthalene had almost returned to planarity (as can be seen in Fig. 8).

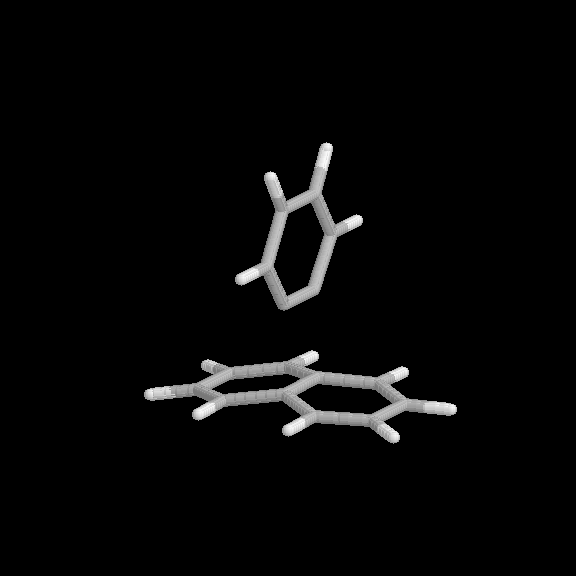
Fig. 8 Partially dissociated benzyne-naphthalene [2+2] adduct. Benzyne pulled back 0.4 Å from equilibrium value.

The geometries of the [2+2] and [2+4] benzyne-C60 adducts are shown in Fig. 4 and 5, respectively. Two view are given for each product. The relative binding energies are given in Table 1. In this case, the [2+2] product is considerably more strongly bound than the [2+4] product, also consistent with the experimental observations.

Finally, the benzyne-nanotube adducts are shown in Fig. 6 and 7 and their relative energies given in Table 1. In contrast to the other systems studied, both products are strongly bound. However, the [2+4] product is more stable than the [2+2].