Automatic molecular design using evolutionary techniques
Al Globus, MRJ Technology Solutions, Inc. at NASA Ames Research
Center
John Lawton, University of California at Santa Cruz
Todd Wipke, University of California at Santa Cruz
Abstract
Molecular nanotechnology is the precise, three-dimensional control of materials
and devices at the atomic scale. An important part of nanotechnology is
the design of molecules for specific purposes. This paper describes early
results using genetic software techniques to automatically design molecules
under the control of a fitness function. The fitness function must be capable
of determining which of two arbitrary molecules is better for a specific
task. The software begins by generating a population of random molecules.
The individual molecules in a population are then evolved towards greater
fitness by randomly combining parts of the better existing molecules to
create new molecules. These new molecules then replace some of the less
fit molecules in the population. We apply a unique genetic crossover operator
to molecules represented by graphs, i.e., sets of atoms and the bonds that
connect them. We present evidence suggesting that crossover alone, operating
on graphs, can evolve any possible molecule given an appropriate fitness
function and a population containing both rings and chains. Most prior
work evolved strings or trees that were subsequently processed to generate
molecular graphs. In principle, genetic graph software should be able to
evolve other graph-representable systems such as circuits, transportation
networks, metabolic pathways, and computer networks.
Introduction
Design problem
Many problems associated with the development of nanotechnology require
custom designed molecules. Frequently it is possible to precisely define
what a molecule must do and still have significant problems designing a
molecule to do the task. Therefore, a design technique to automatically
generate candidate molecules given requirements may be useful. Genetic
algorithms [Holland 75], genetic programming [Koza 92] and genetic graphs
can automatically generate solutions to problems given a function that
determines which of two candidate solutions is better. Genetic algorithms
evolve strings. Genetic programming evolves tree-structured programs. Genetic
graphs evolves graphs (as in graph theory, not xy plots). There are several
classes of molecular nanotechnology designs that can be described as graphs;
i.e., a set of vertices and a set of edges each of which connects two vertices.
Molecules can be described as a set of atoms (vertices) connected by a
set of bonds (edges). Analog circuits can be described as a set of vertices
(nodes) connected by a set of wires or components (edges). Digital circuits
and, presumably, future nanoelectronic circuits can be similarly described.
An automated system for designing graphs with desirable properties should
therefore be able, at least in principle, to design a variety of molecular
nanotechnology systems. In this paper we focus on validation
of the methodology by evolving small molecules; in particular, pharmaceutical
drugs.
Although drug design is not usually considered molecular nanotechnology,
this is a misconception that presumably started because the earliest nanotechnology
work focused on systems analogous to macroscopic machines. Drugs are generally
small molecules. It is known that some drugs fit precisely into receptor
sites to block molecular processes in the body. This must be accomplished
without fitting the receptor sites of the body’s healthy molecular machinery.
Furthermore, drug molecules must survive in the body long enough to be
effective. Early drug discovery was accomplished without understanding
these mechanisms, but modern drug designers often consciously create molecules
with atomic precision to bind well to receptor sites. This is atomically
precise, three-dimensional control of biological devices; i.e., molecular
nanotechnology.
One approach to drug design is to find molecules similar to good drugs
that have fewer negative side effects. Ideally, a candidate replacement
drug is sufficiently similar to have the same beneficial effect but is
different enough to avoid the side effects. In any case, to use genetic
graphs for similarity-based drug discovery we need a good similarity measure
that can score any molecule. [Carhart 85] defined such a similarity measure,
all-atom-pairs-shortest-path, and searched a large database for molecules
similar to diazepam.
Note that the problem we are solving here involves constructing molecular
graphs, rather than examining static graphs. Many classic graph theoretical
problems, graph coloring, finding Hamilton circuits, graph isomorphism,
and maximal subgraphs discovery, have been studied in the search literature.
For example, see [Cheeseman 91]. All of these problems investigate
one or more static graphs. Our problem is to find a graph representing
a molecule with desirable properties. Thus, the characteristics of
our search space is quite different from the classic problems in the literature.
There is little or no reason to believe that crossover would be useful
for these classic graph problems. It is possible to view the
molecular design problem as a search of the space of all molecules.
This space can be represented as a graph (see below). However, rather
than determining some property of the graph representing the search space
we simply look for one or more points in the space that possess desirable
properties. For example, molecules that might make good pharmaceutical
drugs.
Genetic software techniques
For an excellent review of evolutionary software techniques as of spring
1997 see [Baeck 97]. We use the term genetic software to mean that subset
of evolutionary software which uses at least some crossover. Genetic software
techniques seek to mimic natural evolution's ability to produce highly
functional objects. Natural evolution produces organisms. Genetic software
produces sets of parameters, programs, molecular designs, and many other
structures. Genetic software usually solves problems by:
-
Randomly generating a population of individual potential solutions.
-
For each new generation, repeatedly selecting parent individuals at
random with a bias towards better individuals and applying transmission
operators that may involve:
-
Crossover: each of two parents is divided into two parts and one part
from each parent is combined into a child.
-
Mutation: a single ‘parent’ is randomly modified to create a child.
-
Reproduction: a single ‘parent’ is copied into the new generation.
-
Continuing until an acceptable solution is found or for a certain number
of generations.
Genetic software techniques differ in the representation of solutions.
Genetic algorithms use strings of symbols for the representation. The crossover
operator breaks strings in half, usually at a random point. Bit strings
are a common representation, but arrays of floating point numbers, special
symbols that generate circuits [Lohn 98], robot commands [Xiao 97], and
many other symbols may be found in the literature. Strings may be of fixed
or variable length.
Genetic programming [Koza 92] uses trees to represent individuals. This
is particularly useful for representing computer programs. For example,
a tree node representing assignment has two child-nodes, one representing
a variable and the other representing a value. The crossover operator exchanges
randomly selected sub-trees between two parent-trees. Trees may be viewed
as graphs without cycles. Many molecules contain cycles, which chemists
call rings. Therefore, any attempt to use genetic programming to design
molecules must have a mechanism to evolve cycles. This is non-trivial when
crossover can replace any sub-tree with some other random sub-tree. After
much thought we were unable to devise a crossover-friendly tree representation
of arbitrary cyclic graphs. Crossover-friendly means that any sub-tree
is a potential crossover point without restriction. Figure 1 depicts crossover
using strings (genetic algorithms), trees (genetic programming) and graphs
(genetic graphs) using our crossover technique.
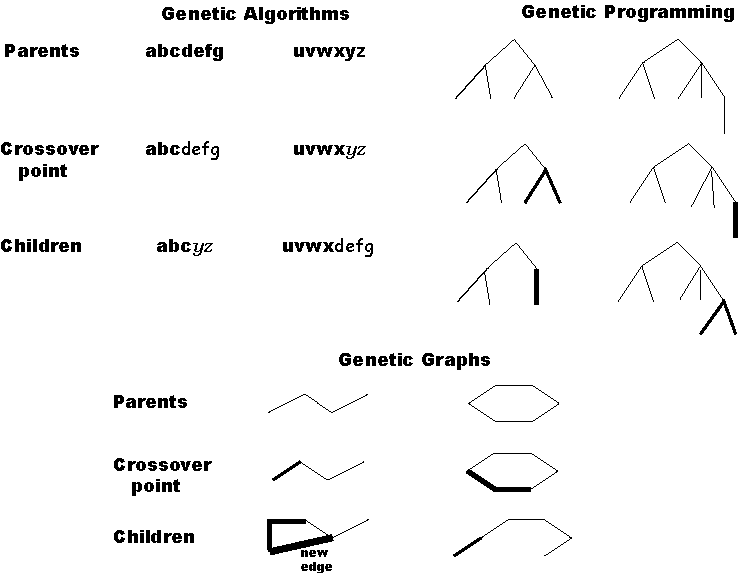
Figure 1: Comparison of crossover operators. The interface
between different font or line thickness indicates the crossover point.
A single crossover point is adequate to divide strings (genetic algorithms)
and trees (genetic programming) into two fragments. Graphs (genetic graphs)
containing cycles require more than one crossover point to divide the system
into two fragments. Furthermore, when two graph fragments with different
numbers of crossover points must be mated, it is possible to create new
edges to satisfy the excess crossover points on one fragment.
Genetic software techniques have been used for molecular design in the
past. There is a patent covering genetic graphs for molecular design [Weininger
95]. The patent describes the straightforward and fairly obvious parts
of mapping standard genetic algorithm techniques to molecular design and
the non-obvious portions: the crossover algorithm and fitness functions.
The crossover algorithm described in the patent uses two parameters: the
digestion rate which breaks bonds, and the dominance rate which apparently
controls how many parts of each parent appear in descendants. This algorithm
may produce fragments rather than completely connected molecules. Our paper
describes a crossover algorithm that always produces connected molecules
and has no parameters. This crossover algorithm is the heart of our genetic
method. Fitness functions are clearly non-obvious, but must usually be
custom designed for each application. Our fitness function and those used
in [Weininger 95] both use the Tanimoto index as a distance measure. [Weininger
95] describes a number of fitness functions. We have used all-pairs-shortest-path
in most of our work. Daylight Chemical Information Systems, Inc., which
holds the patent, reports using genetic techniques to discover lead compounds
for pharmaceutical drug development and other commercial successes.
[Nachbar 98] used genetic programming to evolve molecules for drug design
by sidestepping the crossover/cycles problem. Each tree node represented
an atom with a bond to the parent-node atom and each child-node atom. Hydrogen
atoms were explicitly represented and are always leaf nodes. Rings were
represented by numbering certain atoms and allowing a reference to that
number to be a leaf node. Crossover was constrained not to break or
form rings. Ring evolution was enabled by specific ring opening
and closing mutation operators.
In a personal communication, Astro Teller reported developing a graph
crossover algorithm as part of his dissertation at Carnegie Mellon University.
This technique was applied in Neural Programming, a system developed by
Teller that combines neural nets and genetic programming. At the time this
paper was written, the details of Teller's algorithm were not available
in the literature.
Method
Genetic Graphs
Genetic graphs uses cyclic graphs to represent molecules. Vertices are
typed by atomic elements. Edges can be single, double, or triple bonds.
Valence is enforced. Heavy atoms are explicitly represented by vertices
but hydrogen atoms are implicit; i.e., any heavy atom with unfilled valences
is assumed to be bonded to hydrogen atoms but these are not represented
in the data structure. Our genetic graph software evolves the population
using crossover only; i.e.., mutation and reproduction are not implemented.
These are trivial additions to the method, and we wanted to investigate
the crossover operator first.
Each individual in the initial population is generated by choosing a
random number of atoms between half and twice the number of atoms in the
target molecule. Atoms are randomly chosen from the elements present in
the target molecule. Bonds are then added at random to construct a spanning
tree; i.e., at this point all atoms are connected into a single molecule.
Then a random number of additional bonds are added to create rings. The
type of each bond is selected at random from the set of bond types present
in the target molecule. The number of rings is chosen to be between half
and twice the number of rings in the target molecule. The number of rings,
by our definition, is always = bonds – atoms + 1. For this definition,
single, double, and triple bonds are counted as one bond. In addition,
an unambiguous definition of the number of rings [Corey 69] is used. For
this definition:
-
the set of all rings must include all the bonds participating in any cycle
-
removing any ring will result in at least one bond not being included in
any ring
-
no ring may share more than half its bonds with any other ring
-
the set of rings chosen is at least as large as any other set of rings
with the first three properties
While this definition is precise and useful for coding, it comes to the
interesting conclusion that cubane (a cubic molecule) has five rings, not
six. Consider the six sides of cubane to be six rings in the set of rings.
If any one of the six rings is removed from the set of rings, all bonds
are still included in the set of rings.
For this work, tournament selection was used to choose parents in a
steady state genetic system. Tournament selection means that each parent
is chosen by comparing two randomly chosen individuals and taking the best.
Steady state means that new individuals (children) replace poor individuals
in the population rather than creating a new generation. The poor individuals
are also chosen by tournament, but the worst individual is selected for
replacement. By convention, after population-size individuals have been
replaced, we say that one generation is complete. The implementation follows
this procedure:
-
Generate a random population of molecules
-
Repeat many times, gathering data periodically:
-
Select two molecules from the population at random. Call the better
molecule father.
-
Select two molecules from the population at random. Call the better
molecule mother.
-
Make a copy of father and rip it into two fragments at random.
-
Make a copy of mother and rip it into two fragments at random.
-
Combine one fragment of the copy-of-father and one fragment of the
copy-of-mother into a molecule called son.
-
Combine the other fragment of the copy-of-father and the other fragment
of the copy-of-mother into a molecule called daughter.
-
Choose two molecules from the population at random. Replace the worst
one with son.
-
Choose two molecules from the population at random. Replace the worst
one with daughter.
-
Repeat until satisfied
The most difficult portion of implementing genetic graphs is the crossover
operator described above as "ripping" molecules into two parts and combining
parts from each parent-molecule. Crossover requires two procedures: one
to rip molecules in half and a second to mate two "molecular halves." To
rip a molecule in half we use the following procedure:
-
Choose a random bond
-
Repeat
-
Find the shortest path between the random bond's vertices. The first
time this will be the random bond itself.
-
Remove and remember a random bond from this path. These bonds are called
"cut bonds."
-
Repeat until a cut set is found, i.e., no path exists between the initial
bond's vertices. A cut set is a set of bonds that splits a molecule into
two pieces.
To mate fragments we use the following procedure
-
Repeat
-
Select a random cut bond. Determine which fragment it is associated
with.
-
If at least one cut bond in other fragment exists
-
choose one at random
-
merge the random and selected cut bonds respecting valence
-
Else flip coin
-
if heads -- attach cut bond to random atom in other fragment respecting
valence
-
if tails -- discard cut bond
-
Repeat until each cut bond has been processed exactly once
Figure 2 depicts crossover between butane and benzene to create a
single child.
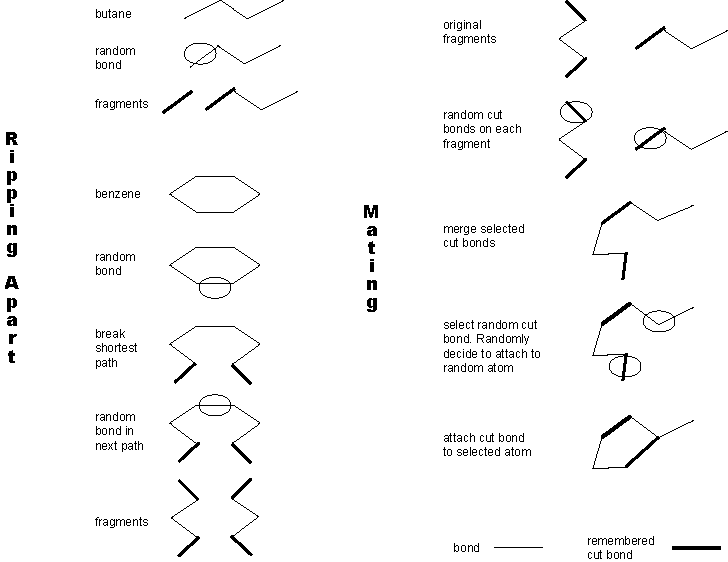
Figure 2: butane and benzene are ripped apart at random points. Then
one fragment of butane and a fragment of benzene are mated. Note that benzene
must be cut in two places. Also, during mating the benzene fragment has
more than one cut bond. A random choice is made to connect this extra cut
bond to a random atom in the butane fragment. Alternatively, the extra
cut bond could have been discarded.
A somewhat more complete but significantly more confusing explanation
follows. The terms vertex and edge are used for atom and bond respectively
to indicate that the algorithm may be applied to any graph structure.
-
Create copies of each parent.
-
Randomly cut each copy into two fragments by selecting a random edge-cut-set
and removing the edges in the cut set from each copy. An edge-cut-set is
a set of edges that, when removed, causes a graph to break into two disconnected
fragments. The cut set is generated by the following procedure:
-
Choose an edge at random.
-
Find the shortest path between the vertices of the edge. A path is
an ordered list of edges, each of which shares a vertex with each neighboring
edge. The first and last edges connect the two vertices of the original
randomly chosen edge.
-
Select a random edge from the path, remove it from the molecule, and
place it in the cut set.
-
Go to 2 until a cut set is found.
-
Combine one fragment of the father's copy with one fragment of the
mother's copy at random by the following procedure:
-
Select a random cut edge (an edge in either cut set). Call this edge’s
vertex in the part to be mated v1.
-
If any compatible (same bond type) cut edge in the other parent-copy-fragment
exists, choose one at random. Call this edge’s vertex in the other part-parent-copy
v2. Connect v1 and v2 with a compatible edge.
-
If no comparable cut edge was found, select a random cut edge in the
other parent-copy-fragment and connect the appropriate vertices with a
new random edge that satisfies valence.
-
If no cut edge is left in the other parent-copy-fragment, flip a virtual
coin. If heads, connect v1 to a random vertex in the other parent-copy-fragment.
-
Go to 1 until all cut edges have been processed exactly once.
This approach can open and close rings using crossover alone and can even
generate cages and higher dimensional graph structures as long as there
are rings in the population. Unfortunately, if there are no rings in the
population none can be generated. Similarly, if the population consists
entirely of rings, no chains can be generated. Also, once the population
consists entirely of two-atom-graphs, no graphs with more than two atoms
can be generated. Nonetheless, this approach is by far the most general
of those we examined or found in the literature. In particular, unlike
[Nachbar 98] no special-purpose ring opening and closing operators are
necessary. Unlike [Weininger 95] no parameters are necessary and multiple
molecular fragments are never produced.
The computational resources required for genetic software to find a
solution is a function of the size of the search space, among other factors.
The space of all possible graphs is combinatorial and enormous. For molecular
design this space can be radically reduced by enforcing valence limits
for each atom. Thus, a carbon atom with one double and two single bonds
will not be allowed to add another bond. Also, avoiding explicit representation
of hydrogen atoms substantially reduces the size of the graph and therefore
the search space.
Molecule Space Characteristics
The space of all molecules has very little in common with a multidimensional
continuous Cartesian space. The space consists of a large number
of discrete points with no derivatives. One may, however, think of
each point as having neighbors so that the space may have local and global
minima. We may define the neighbors of a molecule as all molecules
that may be formed by certain mutations. These mutations are adding
or deleting one bond, adding a bond and an atom, changing an atom type,
or changing a bond type. This scheme is sufficient for a graph to
describe the space of all molecules with a single additional operation
of adding a single atom to the "null molecule," a molecule with no atoms
or bonds.
Fitness function: all-pairs-shortest-path similarity
The key to any genetic software solution is a good fitness function --
for tournament selection a function that can determine if one molecule
is better than another. This function must be very robust since the randomly
generated initial molecules rarely make much chemical sense. Fitness functions
must also make fine distinctions between any two molecules even if both
are very good or very bad. These fine distinctions are necessary to avoid
flat regions in the fitness space where no direction is given to evolution.
Also, for our initial studies we wanted a fitness function that only required
the graph of a molecule, not the xyz coordinates of each atom.This simplifies
initial studies and avoids the necessity of equilibrating the structure
of candidate molecules, a CPU intensive step. The all-atoms-pairs-shortest-path
similarity test chosen [Carhart 85] is a robust graph-only fitness function.
Each atom is given an extended type consisting of the atomic number and
the number of single, double, and triple bonds the atom participates in.
Then the shortest path between each pair of atoms is found. A bag is constructed
with one element for each atom pair. Each element in the bag is represented
by the sorted extended types of the two atoms and the length of the shortest
path between them. The fitness of each candidate molecule is the distance
between its bag and the similarly constructed bag of a target molecule.
A bag is a set that allows duplicate elements.
The distance measure used is the Tanimoto index. This is
|a intersection b| / |a union b|
where a is the candidate’s bag and b is the target’s bag. Two elements
are considered identical for the purpose of the intersection and union
operations if the atoms have the same extended types and the distance between
them is identical. Each duplicate in the bag is considered a separate element
for the purpose of intersection and union operators. This measure always
returns a number between 0 and 1. We prefer fitness functions that return
lower numbers for fitter individuals, so we subtract the Tanimoto index
from one.
Search spaces with many local minima are difficult to search because
many algorithms tend to converge to local minima and miss the global minimum.
The all-pairs-shortest-path fitness function has many local minima over
the space of all molecules whenever the target molecule contains rings.
Consider benzene, a six membered ring, as the target molecule. Any ring
other than a six membered ring will be at a local minimum because a bond
must be removed, lowering the fitness in most cases, before bonds and atoms
can be added to generate benzene. Thus, any target molecule containing
rings will have associated search space containing many local minima. Interestingly,
a small modification in the definition of the molecular search space eliminates
the local minima. Consider mutations that replace an edge with a
vertex and two edges and replace a vertex and two edges with one edge.
These mutations can change the size of rings. If these mutations can create
neighbors in the space of all molecules, then incorrectly sized rings are
not local minima. While we think these additional neighbor definitions
are unreasonable, they do illustrate the difficulty of understanding the
space of all molecules.
The targets for our initial study were butane, benzene, cubane, purine,
diazepam, morphine and cholesterol. All targets except butane contain rings
and thus generate a search space with local minima. The fitness function
can not only find similar molecules, which is useful in drug design, but
can also lead evolution to the exact molecule used as a target. This proves
that the algorithm can reach particular kinds of molecules and the number
of generations to find the target provides a quantitative measure of performance.
Unfortunately, our implementation of all-pairs-shortest-path is O(n3)
so finding larger molecules can be quite time consuming.
Implementation
The genetic graphs program is implemented in Java. Java was chosen since
its syntax is similar to C++, many useful libraries are available, garbage
collection vastly simplifies memory management, and Java’s array bounds
testing and other bug-reducing features substantially reduce debugging
time and produce more robust code than C++, Fortran or C. A significant
run-time penalty is paid for these advantages. With luck, future improvements
in Java development and run-time environments will reduce the performance
penalty. All production runs were executed on SGI workstations at the NAS
Division of NASA Ames Research Center.
Test environment
According to our hypothesis, genetic graphs algorithm can find any possible
molecule. To partially test this hypothesis, we ran the program using several
target molecules:
-
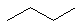 butane (C4H10)
a simple linear molecule.
butane (C4H10)
a simple linear molecule.
-
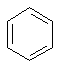 benzene
(C6H6) a simple molecule with a ring.
benzene
(C6H6) a simple molecule with a ring.
-
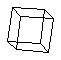 cubane (C8H8)
a cage molecule.
cubane (C8H8)
a cage molecule.
-
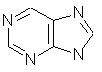 purine (C5H4N4)
fused rings and heteroatoms.
purine (C5H4N4)
fused rings and heteroatoms.
-
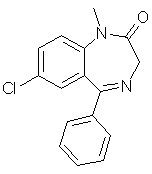 diazepam (C16H13ClN2O)
used in [Carhart 85].
diazepam (C16H13ClN2O)
used in [Carhart 85].
-
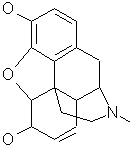 morphine (C17H19NO3)
Dr. Wipke's group has worked on morphine analog design for many years.
morphine (C17H19NO3)
Dr. Wipke's group has worked on morphine analog design for many years.
-
 cholesterol
(C27H46O) a non-drug molecule.
cholesterol
(C27H46O) a non-drug molecule.
Stereochemistry and hydrogens are left out of the molecular diagrams
since the software does not consider them.
Since the algorithm is stochastic, twenty runs were conducted for each
target molecule. The number of generations and population size were varied
in an attempt to have enough successful runs (at least 11) to calculate
the median time to find the target. Once the target was found the run stopped.
Runs also stopped after a fixed, maximum number of generations. A few of
the best individuals were saved to see if the software produced molecules
similar to the target. These may be useful for drug design.
Results
| 20 runs for each molecule |
Population size |
Median generations to find target |
Minimum generations to find target |
Number of runs that failed to find target |
Maximum generations
|
| Benzene |
200
|
39.5
|
2
|
8
|
1000
|
| Cubane |
100
|
46.5
|
13
|
0
|
1000
|
| Purine |
100
|
245.0
|
19
|
4
|
1000
|
Median, rather than mean, generations to find the target was chosen because
the data varied widely and many runs did not complete [Claerbout 73]. Butane
was usually found in the initial random population so data were not taken.
With a population of 100, the benzene runs did not find the target often
enough to calculate the median so the larger population size was used.
At the time of writing, there was not sufficient data for diazepam, morphine,
or cholesterol to calculate the median for twenty runs. However, each molecule
has been found at least once:
| Molecule |
Population size |
Generation found |
Fitness function |
| Morphine |
1000
|
208
|
all-pairs-shortest-path |
| Diazepam |
200
|
256
|
all-pairs-shortest-path |
| Cholesterol minus the two methyl groups connected to the rings |
500
|
1765
|
all-pairs-shortest-path plus number of rings |
The modified cholesterol was used due to an error in the input file. Although
cholesterol was not found, the molecule that was found is very similar.
To see if the crossover operator was better than random search, we searched
for purine under three conditions: crossover alone, generating random molecules
using the same algorithm as for the initial population (random search),
and a 50-50 mix of crossover and random search. Twenty-one runs of
1000 generations on a population of 200 were conducted in each case.
| case |
number of runs that found purine |
median generations to find purine |
| random search |
0
|
N/A
|
| crossover alone |
21
|
37
|
| 50-50 mix of crossover and random search |
21
|
48
|
Clearly the crossover operator is better than random search.
Discussion
The genetic graphs algorithm can clearly find small molecules given an
appropriate fitness function, and can find more complex molecules although
significant time is required. The variability of runs is remarkable. Note
that eight runs failed to find benzene in 1000 generations, but one run
found benzene in only two generations. A few of the 20 runs found benzene
in only three generations. It’s also interesting to note that cubane was
always found although the median time to discovery was somewhat greater
than for benzene; and the cubane run used a smaller population. Presumably,
cubane's single bond type simplified the search. Finally, note the much
larger median time to success for purine. Apparently the addition of nitrogen
and the fused ring made finding the target significantly more difficult.
Still, more purine runs were successful than benzene runs.
Finding moderate size molecules has proven difficult with the available
computer resources. This is probably because our fitness function was O(n3),
but also due to problems with the cycle-stealing batch system used to run
this program on idle workstations. Most genetic software uses mutation
as well as crossover. Mutation helps systems make small changes. While
crossover seems to be capable of generating molecules, the performance
is sufficiently poor that mutation operators might help a great deal. Other
than the usual operators to add and remove atoms or bonds, it may be helpful
to have a mutation operator that makes a random ring aromatic (alternating
double and single bonds for certain sized rings). Generating aromatic rings
with crossover alone is probably difficult (note the problems generating
benzene) so a special mutation operator may be helpful.
Examining populations generated by diazepam, cholesterol, and morphine
we noted that the best molecules all had the same ring structure. This
did not appear to be true of the population as a whole. Thus, it
is possible for the population to get stuck in local minima. Occasionally
the best molecule in a population would be radically improved by a particularly
fortuitous crossover, but this can take a long time. We found that a minor
modification to the fitness function eliminated this difficulty in the
cholesterol run. The fitness function was an equal combination of all-pairs-shortest-path
and a modified Tanimoto index on the number of rings in the target molecule
versus the candidate. This fitness function appears to do a better job
of finding interesting analogues to the target molecule by keeping the
ring structure diverse. With all-pairs-shortest-path alone, populations
seem to converge on a single poor ring structure, at least for the best
molecules in the population. Adding the distance between the number of
rings generates more fit molecules and more diverse ring structures, at
least in preliminary results.
Performance analysis demonstrates what might be expected — our O(n3)
fitness function took most of the CPU time. A faster fitness function would
substantially speed calculations. Some runs with faster fitness functions
have been made, but these simpler fitness functions do not drive evolution
to find the target exactly so comparison with the above data is difficult.
Genetic software lore suggests that the fitness function is exceptionally
important [Kinnear 94]. Our results bear this out.
Fortunately, the algorithm is embarrassingly parallel since many runs
are required. Also, there is significant potential for parallelism within
runs since fitness function execution on each individual is completely
independent. Furthermore, the algorithm can be easily restarted and can
afford to lose some runs. Thus, genetic graphs is a good candidate for
cycle-scavenging batch systems such as Condor [Litzkow
88]. Large genetic graph production runs can therefore
use otherwise wasted workstation and PC cycles at facilities with large
numbers of these machines. Although some of the results presented here
were simply run on workstations, all current jobs are run under Condor.
Searching for Molecules
Molecular design may be viewed as searching the space of all possible molecules
for molecules with particular properties. One might expect genetic
graphs to have strengths and weaknesses similar to genetic algorithms applied
to other problems. Most research to determine which problems are
difficult for genetic algorithms has focused on "deception," where partial
solutions to a problem point away from the full solution [Goldberg 89].
[Forrest 93] points out, however, that
"... deception is not the only factor determining how hard
a problem will be for a GA (genetic algorithm), it is not even clear what
the relation is between the degree of deception in a problem and the problem's
difficulty for the GA. There are a number of factors that can make
a problem easy or hard, including those we described in this article: the
presence of multiple conflicting solutions or partial solutions, the degree
of overlap, and the amount of information from lower-order building blocks
(as opposed to whether or not this information is misleading). Other
factors include sample error [Grefenstette 89], the number of local optima
in the landscape [Schaeffer 89], and the relative differences in fitness
between disjointed desirable schemas [Mitchell 92]. Most efforts
at characterizing the ease or difficulty of problems for the GA have concentrated
on deception, but these other factors have to be taken into account as
well.
"At present, the GA community lacks a coherent theory of the effects
on the GA of the various sources of facilitation or difficulty in a given
problem; we also lack a complete list of such sources, as well as an understanding
of how to define and measure them. Until such a theory is developed,
the terms 'GA-hard' and 'GA-easy' should be defined in terms of the GA's
performance on the given problem rather than in terms of the a priori
structure of the problem." (formatting modified to fit the conventions
of this paper)
The primary contribution of this paper is the creation of a crossover operator
for graphs. This allows the use of genetic algorithm techniques using
graph representations. As [De Jong 90] states:
"The key point in deciding whether or not to use genetic algorithms
for a particular problem centers around the question: what is the space
to be searched? If that space is well-understood and contains structure
that can be exploited by special-purpose search techniques, the use of
genetic algorithms is generally computationally less efficient. If
the space to be searched is not so well understood, and relatively unstructured,
and if an effective GA representation of that space can be developed,
then GAs provide a surprisingly powerful search technique for large, complex
spaces." (italics added by [Forrest 93])
Chemists have known for over a century that graphs are the most natural
representation of molecules. Furthermore, the space of molecules is not
well understood or characterized. Therefore, it is reasonable to
presume that searching the space of molecules using genetic graphs
will be profitable in a number of domains. We hope that our crossover
operator will make a contribution.
Future work
Although finding target molecules is a useful measure of the algorithm,
we already know the target molecule. The real purpose of the similarity
fitness function is to find molecules similar but not identical to the
target. In particular, the ideal result is a wide variety of molecules
dissimilar to each other but relatively similar to the target molecule.
This provides a diverse set of candidate molecules for drug development,
a process that takes millions of dollars and many years to complete. In
the ideal case, one or more candidates will have the beneficial properties
of the target without negative side effects. Preliminary analysis of collections
of the best individuals from each generation suggests that these collections
are quite diverse and share some of the properties of the target molecule.
Most of the analog molecules found tend to be chemically unstable in physiological
conditions. We are developing a fitness function that will penalize molecules
that are unstable in the body.
Many fitness functions of interest require molecular conformation; i.e.,
xyz coordinates for each atom. For example, designing a molecule to fit
in a protein receptor to inhibit the activity of a disease organism, as
the new and fairly effective AIDS drugs do, require molecular conformation.
To design a fitness function evolving molecular fit, the very bizarre molecules
often created by crossover must have their energy minimized quickly. Most
minimizers available today will not work well with without a "reasonable"
start point. We are searching the literature for algorithms to minimize
very "bad" molecules. Searching for molecules when conformation is important
may be expected to be more difficult than the search is described in this
paper. Energy minimization takes considerable CPU time, multiple
conformations for molecules increase the size of the search space, and
a different crossover operator that takes physical space into consideration
may be necessary.
It may be possible to search for molecules using hill climbing algorithms.
However, the space of all molecules has no derivatives and no orthogonal
dimensions. Therefore, from each molecule one must examine all the
neighbors to find the steepest hill to climb. Since even moderately
sized molecules will have a huge number of neighbors in the molecular space
defined above, hill climbing algorithms are expected to have great difficulties.
It may be possible, however, to use hill climbing algorithms that climb
any reasonable hill rather than the steepest one. This amounts to evolution
using mutation where only profitable mutations are allowed to survive.
We hope to test this technique in the near future.
Circuit design is another field for which genetic graphs should, in
principle, be well suited. Genetic algorithms (using variable length strings)
[Lohn 98] and genetic programming [Koza 97] have been used to design analog
circuits. In the genetic programming case, a tree language to generate
analog circuits compatible with the SPICE (Simulation Program with Integrated
Circuit Emphasis) [Quarles 94] simulator was constructed and a 64 node
(80MHz per node) parallel supercomputer was used to design the circuits.
The system designed a lowpass filter, a crossover filter, a four-way source
identification circuit, a cube root circuit, a time-optimal controller
circuit, a 100 dB amplifier, a temperature-sensing circuit, and a voltage
reference source circuit. Thus, genetic programming can design graph-structured
systems. However, we have found it extremely difficult to create a tree
language that can generate any possible graph and support crossover cleanly.
Therefore, it may be advantageous to directly evolve graphs rather than
trees that represent cyclic graphs.
Finally, it might be interesting to explore the relationship between
genetic graphs, applied to molecules, and combinatorial chemistry.
Combinatorial chemistry is a new field undergoing rapid development where
hundreds or thousands of molecules and simultaneously manipulated and examined.
The recombination rules in genetic graphs are not constrained by physical
reality, whereas reactions in combinatorial chemistry experiments clearly
are. Combinatorial chemistry is also much faster than genetic graphs, even
on massively parallel computers. Crossover and fitness function evaluation
can take seconds or even minutes on a workstation, but thousands of simultaneous
reactions can occur on a much smaller time scale.
Summary
Algorithms and software to evolve graphs using genetic techniques were
developed and applied to drug design using a molecular similarity based
fitness function. Early data suggest that the software can indeed discover
a variety of small molecules. Significant additional work will be required
to demonstrate that representing molecules as graphs and using genetic
software techniques is of major benefit in molecular design.
Acknowledgments
Thanks to Rich McClellan for providing the mol file reading and atomic
element code. Thanks to Creon Levit, Subash Saini, and Meyya Meyyapan of
NASA Ames for their support. Thanks to Creon Levit, Jason Lohn and
Bonnie Klein for reviewing this paper. Special thanks to the anonymous
referee who pointed us to many important results in the search literature.
This work was funded by NASA Ames contract NAS 2-14303.
References
[Baeck 97] Thomas Baeck, Ulrich Hammel, and Hans-Paul Schwefel, "Evolutionary
computation: comments on the history and current state," IEEE Transactions
on Evolutionary Computation, volume 1, number 1, pages 3-17, April
1997.
[Carhart 85] Raymond Carhart, Dennis H. Smith, and R. Venkataraghavan,
"Atom pairs as molecular features in structure-activity studies: definition
and application," Journal of Chemical Information and Computer Science,
23, pages 64-73, 1985.
[Cheeseman 91] Peter Cheeseman, Bob Kanefsky, William M. Taylor, "Where
the Really Hard Problems Are," Proceedings of the 12th International
Conference on Artificial Intelligence, Darling Harbor, Sydney, Australia,
24-30 August 1991.
[Claerbout 73] J. F. Claerbout and F. Muir, ``Robust Modeling with Erratic
Data,'' Geophysics, 38, pages 826-844, 1973.
[Corey 69] E. J. Corey and W. Todd Wipke, "Computer-Assisted Design
of Complex Organic Syntheses," Science, volume 166, pages 178-192,
10 October 1969.
[De Jong 90] K. A. De Jong "Introduction to the Second Special
Issue on Genetic Algorithms," Machine Learning, 5 (4), 1990.
[Forrest 93] Stephanie Forrest and Melanie Mitchell, "What Makes a Problem
Hard for Genetic Algorithm? Some Anomalous Results in the Explanation,"
Machine Learning, 13, pages 285-319, 1993.
[Goldberg 89] David E. Goldberg, Genetic Algorithms in Search, Optimization,
and Machine Learning, Addison-Wesley Publishing Co., Inc., 1989.
[Grefenstette 89] J. J. Grefenstette and J. E. Baker, "How Genetic Algorithms
Work: A Critical Look at Implicit Parallelism," Proceedings of the Third
International Conference on Genetic Algorithms, J. D. Schaffer, Editor,
San Mateo, CA, Morgan Kaufmann, 1989.
[Holland 75] John H. Holland, Adaptation in Natural and Artificial
Systems, University of Michigan Press, 1975.
[Kinnear 94] Kenneth E. Kinnear, Jr., "A perspective on the work in
this book," Advances in Genetic Programming, edited by Kenneth E.
Kinnear, Jr., MIT Press, Cambridge, Massachusetts, pages 3-20, 1994.
[Koza 92] John R. Koza, Genetic Programming: on the Programming of
Computers by Means of Natural Selection, MIT Press, Massachusetts,
1992.
[Koza 97] John R. Koza, Forrest H. Bennett III, David Andre, Martin
A. Keane and Frank Dunlap, "Automated synthesis of analog electrical circuits
by means of genetic programming," IEEE Transactions on Evolutionary
Computation, volume 1, number 2, pages 109-128, July 1997.
[Litzkow 88] M. Litzkow, M. Livny, and M. W. Mutka, "Condor - a hunter
of idle workstations,'' Proceedings of the 8th International Conference
of Distributed Computing Systems, pp. 104-111, June1988. See http://www.cs.wisc.edu/condor/.
[Lohn 98] Jason D. Lohn and Silvano P. Colombano, "Automated analog
circuit synthesis using a linear representation,'' Second International
Conference on Evolvable Systems: From Biology to Hardware, Springer-Verlag,
Sept.23-25, 1998. (to appear)
[Mitchell 92] M. Mitchell, S. Forrest, and J. H. Holland, "The Royal
Road Genetic Algorithms: Fitness Landscapes and GA Performance," Proceedings
of the First European Conference and Artificial Life, Cambridge, MA,
MIT Press/Branford Books, 1992.
[Nachbar 98] Robert B. Nachbar, "Molecular evolution: a hierarchical
representation for chemical topology and its automated manipulation," Proceedings
of the Third Annual Genetic Programming Conference, University of Wisconsin,
Madison, Wisconsin, 22-25 July 1998, pages 246-253.
[Quarles 94] T. Quarles, A. R. Newton, D. O. Pederson, and A. Sangiovanni-Vincentelli,
SPICE 3 Version 3F5 User's Manual, Department of Electrical Engineering
and Computer Science, University of California at Berkeley, CA, March 1994.
[Schaeffer 89] J. D. Schaffer, Editor, Proceedings of the Third
International Conference on Genetic Algorithms, San Mateo, CA, Morgan
Kaufmann, 1989.
[Weininger 95] David Weininger, "Method and apparatus for designing
molecules with desired properties by evolving successive populations,"
U.S. patent US5434796, Daylight Chemical Information Systems, Inc.
1995.
[Xiao 97] Jiang Xiao, Zbigniew Michalewicz, Lixin Zhang, and Krzysztof
Trojanowski, "Adaptive evolutionary planner/navigator or mobile robots,"
IEEE Transactions on Evolutionary Computation, volume 1, number
1, pages 18-28, April 1997.


 benzene
(C6H6) a simple molecule with a ring.
benzene
(C6H6) a simple molecule with a ring. cubane (C8H8)
a cage molecule.
cubane (C8H8)
a cage molecule. purine (C5H4N4)
fused rings and heteroatoms.
purine (C5H4N4)
fused rings and heteroatoms. diazepam (C16H13ClN2O)
used in [Carhart 85].
diazepam (C16H13ClN2O)
used in [Carhart 85]. morphine (C17H19NO3)
Dr. Wipke's group has worked on morphine analog design for many years.
morphine (C17H19NO3)
Dr. Wipke's group has worked on morphine analog design for many years. cholesterol
(C27H46O) a non-drug molecule.
cholesterol
(C27H46O) a non-drug molecule.